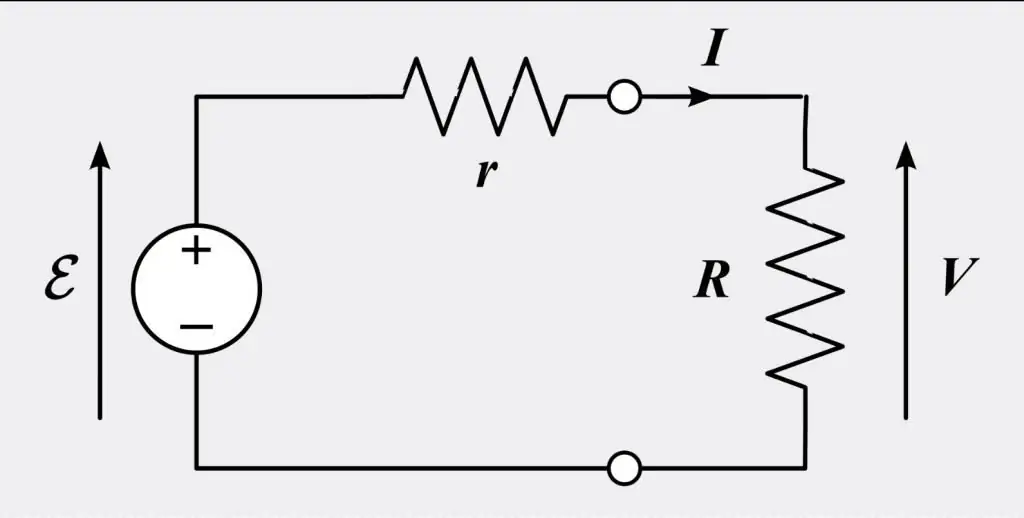
Ohm se wet in differensiële en integrale vorm bepaal dat die stroom deur 'n geleier tussen twee punte direk eweredig is aan die spanning by die twee punte. 'n Vergelyking met 'n konstante lyk soos volg:
I=V/R, waar I die punt van stroom deur die geleier in eenhede van ampère is, V (Volt) is die spanning gemeet met die geleier in eenhede van volt, R is die weerstand van die materiaal wat gelei word in ohm. Meer spesifiek stel Ohm se wet dat R 'n konstante in hierdie opsig is, onafhanklik van stroom.
Wat kan onder "Ohm se wet" verstaan word?
Ohm se wet in differensiële en integrale vorm is 'n empiriese verwantskap wat die geleidingsvermoë van die oorgrote meerderheid geleidende materiale akkuraat beskryf. Sommige materiale gehoorsaam egter nie Ohm se wet nie, dit word "nie-ohmies" genoem. Die wet is vernoem na die wetenskaplike Georg Ohm, wat dit in 1827 gepubliseer het. Dit beskryf spanning- en stroommetings met behulp van eenvoudige elektriese stroombane wat bevatverskillende draadlengtes. Ohm het sy eksperimentele resultate verduidelik met 'n effens meer komplekse vergelyking as die moderne vorm hierbo.
Die konsep van Ohm se wet in verskil. vorm word ook gebruik om verskeie veralgemenings aan te dui, byvoorbeeld, die vektorvorm daarvan word in elektromagnetisme en materiaalwetenskap gebruik:
J=σE, waar J die aantal elektriese deeltjies op 'n spesifieke plek in die weerstandsmateriaal is, e die elektriese veld by daardie plek is, en σ (sigma) die materiaal is wat afhanklik is van die geleidingsvermoë parameter. Gustav Kirchhoff het die wet presies so geformuleer.
Geskiedenis

Geskiedenis
In Januarie 1781 het Henry Cavendish geëksperimenteer met 'n Leyden-kruik en 'n glasbuis van verskillende deursnee gevul met 'n soutoplossing. Cavendish het geskryf dat spoed direk verander as die graad van elektrifisering. Aanvanklik was die resultate onbekend aan die wetenskaplike gemeenskap. Maar Maxwell het hulle in 1879 gepubliseer.
Ohm het sy werk oor weerstand in 1825 en 1826 gedoen en sy resultate in 1827 gepubliseer in "The Galvanic Circuit Proved Mathematically". Hy is geïnspireer deur die werk van die Franse wiskundige Fourier, wat hittegeleiding beskryf het. Vir eksperimente het hy aanvanklik galvaniese pale gebruik, maar later oorgeskakel na termokoppels, wat 'n meer stabiele spanningsbron kon verskaf. Hy het met die konsepte van interne weerstand en konstante spanning gewerk.
Ook in hierdie eksperimente is 'n galvanometer gebruik om die stroom, sedert die spanning, te meettussen termokoppelterminale eweredig aan die verbindingstemperatuur. Hy het toe toetskabels van verskillende lengtes, diameters en materiale bygevoeg om die stroombaan te voltooi. Hy het gevind dat sy data gemodelleer kan word met die volgende vergelyking
x=a /b + l, waar x die meterlesing is, l die lengte van die toetsleiding is, a afhanklik is van die temperatuur van die termokoppelaansluiting, b 'n konstante (konstante) van die hele vergelyking is. Ohm het sy wet op grond van hierdie proporsionaliteitsberekeninge bewys en sy resultate gepubliseer.
Belangrikheid van Ohm se wet
Ohm se wet in differensiële en integrale vorm was waarskynlik die belangrikste van die vroeë beskrywings van die fisika van elektrisiteit. Vandag beskou ons dit amper vanselfsprekend, maar toe Om sy werk die eerste keer gepubliseer het, was dit nie die geval nie. Kritici het met vyandigheid op sy interpretasie gereageer. Hulle het sy werk "naakte fantasieë" genoem en die Duitse minister van onderwys het verklaar dat "'n professor wat sulke dwaalleer verkondig, onwaardig is om wetenskap te onderrig."
Die heersende wetenskaplike filosofie in Duitsland het destyds gemeen dat eksperimente nie nodig was om 'n begrip van die natuur te ontwikkel nie. Daarbenewens het Geogr se broer, Martin, 'n wiskundige van beroep, met die Duitse onderwysstelsel gesukkel. Hierdie faktore het die aanvaarding van Ohm se werk verhinder, en sy werk het eers in die 1840's algemeen aanvaar. Nietemin het Om lank voor sy dood erkenning ontvang vir sy bydraes tot die wetenskap.
Ohm se wet in differensiële en integrale vorm is 'n empiriese wet,veralgemening van die resultate van baie eksperimente, wat getoon het dat die stroom ongeveer eweredig is aan die elektriese veldspanning vir die meeste materiale. Dit is minder fundamenteel as Maxwell se vergelykings en is nie geskik in alle situasies nie. Enige materiaal sal afbreek onder die krag van 'n voldoende elektriese veld.
Ohm se wet is op 'n wye reeks skale waargeneem. Aan die begin van die 20ste eeu is Ohm se wet nie op 'n atoomskaal beskou nie, maar eksperimente bevestig die teendeel.
Quantum Beginning
Die afhanklikheid van die stroomdigtheid van die toegepaste elektriese veld het 'n fundamenteel kwantummeganiese karakter (klassieke kwantumdeurlaatbaarheid).’n Kwalitatiewe beskrywing van Ohm se wet kan gebaseer word op klassieke meganika deur gebruik te maak van die Drude-model wat in 1900 deur die Duitse fisikus Paul Drude ontwikkel is. As gevolg hiervan het Ohm se wet baie vorme, soos die sogenaamde Ohm se wet in differensiële vorm.
Ander vorme van Ohm se wet
Ohm se wet in differensiële vorm is 'n uiters belangrike konsep in elektriese/elektroniese ingenieurswese omdat dit beide spanning en weerstand beskryf. Dit alles is op makroskopiese vlak met mekaar verbind. Wanneer elektriese eienskappe op die makro- of mikroskopiese vlak bestudeer word, word 'n meer verwante vergelyking gebruik, wat "Ohm se vergelyking" genoem kan word, met veranderlikes wat nou verwant is aan die skalêre veranderlikes V, I en R van Ohm se wet, maar wat is 'n konstante funksie van posisie inontdekkingsreisiger.
Effek van magnetisme

As 'n eksterne magneetveld (B) teenwoordig is en die geleier is nie in rus nie, maar beweeg teen 'n spoed V, dan moet 'n bykomende veranderlike bygevoeg word om rekening te hou met die stroom wat deur die Lorentz-krag op die lading geïnduseer word. draers. Ook genoem Ohm se wet van integrale vorm:
J=σ (E + vB).
In die rusraam van 'n bewegende geleier word hierdie term laat val omdat V=0. Daar is geen weerstand nie omdat die elektriese veld in die rusraam verskil van die E-veld in die laboratoriumraam: E'=E + v × B. Elektriese en magnetiese velde is relatief. As J (stroom) veranderlik is omdat die toegepaste spanning of E-veld met tyd wissel, moet reaktansie by die weerstand gevoeg word om self-induksie in ag te neem. Die reaktansie kan sterk wees as die frekwensie hoog is of die geleier gewikkel is.






