Ohm se wet is die basiese wet van elektriese stroombane. Terselfdertyd laat dit ons toe om baie natuurlike verskynsels te verduidelik.’n Mens kan byvoorbeeld verstaan hoekom elektrisiteit nie die voëls wat op die drade sit “klop” nie. Vir fisika is Ohm se wet uiters betekenisvol. Sonder sy medewete sou dit onmoontlik wees om stabiele elektriese stroombane te skep of daar sou glad nie elektronika wees nie.
Afhanklikheid I=I(U) en die waarde daarvan
Die geskiedenis van die ontdekking van die weerstand van materiale hou direk verband met die stroomspanning-eienskap. Wat dit is? Kom ons neem 'n stroombaan met 'n konstante elektriese stroom en oorweeg enige van sy elemente: 'n lamp, 'n gaspyp, 'n metaalgeleier, 'n elektrolietfles, ens.
Deur die spanning U (dikwels na verwys as V) te verander wat aan die betrokke element verskaf word, sal ons die verandering in die sterkte van die stroom (I) wat daardeur gaan, opspoor. As gevolg hiervan kry ons 'n afhanklikheid van die vorm I \u003d I (U), wat die "spanningskenmerk van die element" genoem word en is 'n direkte aanduiding van syelektriese eienskappe.
V/A-kenmerk kan anders lyk vir verskillende elemente. Die eenvoudigste vorm daarvan word verkry deur 'n metaalgeleier te oorweeg, wat deur Georg Ohm (1789 - 1854) gedoen is.
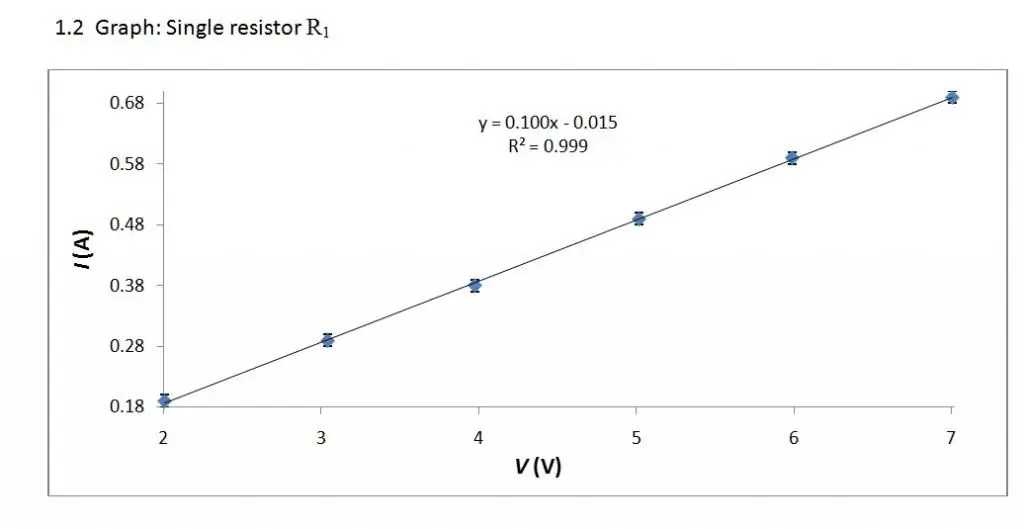
Volt-ampere-kenmerk is 'n lineêre verwantskap. Daarom is sy grafiek 'n reguit lyn.
Die wet in sy eenvoudigste vorm
Ohm se navorsing oor die stroomspanning-eienskappe van geleiers het getoon dat die stroomsterkte binne 'n metaalgeleier eweredig is aan die potensiaalverskil aan sy ente (I ~ U) en omgekeerd eweredig aan 'n sekere koëffisiënt, dit wil sê I ~ 1/R. Hierdie koëffisiënt het bekend geword as "geleierweerstand", en die meeteenheid van elektriese weerstand was Ohm of V/A.
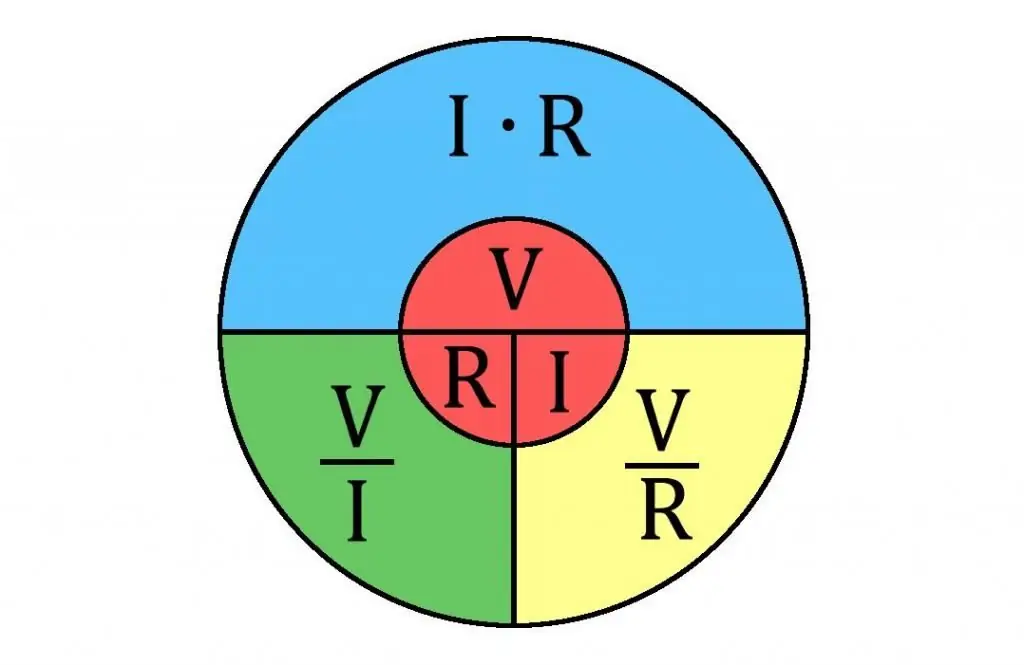
Nog een ding om op te let. Ohm se wet word dikwels gebruik om weerstand in stroombane te bereken.
Wetbewoording
Ohm se wet sê dat die stroomsterkte (I) van 'n enkele gedeelte van die stroombaan eweredig is aan die spanning in hierdie gedeelte en omgekeerd eweredig aan sy weerstand.
Daar moet op gelet word dat die wet in hierdie vorm slegs waar bly vir 'n homogene deel van die ketting. Homogeen is daardie deel van die elektriese stroombaan wat nie 'n stroombron bevat nie. Hoe om Ohm se wet in 'n inhomogene stroombaan te gebruik, sal hieronder bespreek word.
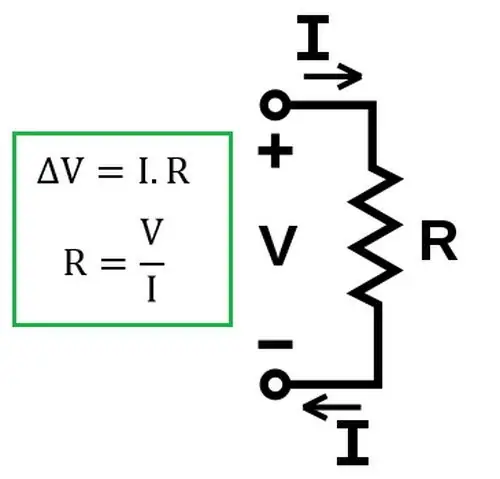
Later is eksperimenteel vasgestel dat die wet geldig bly vir oplossingselektroliete in 'n elektriese stroombaan.
Fisiese betekenis van weerstand
Weerstand is 'n eienskap van materiale, stowwe of media om die deurgang van elektriese stroom te voorkom. Kwantitatief beteken 'n weerstand van 1 ohm dat in 'n geleier met 'n spanning van 1 V aan sy ente 'n elektriese stroom van 1 A kan verbygaan
Elektriese weerstand
Eksperimenteel is gevind dat die weerstand van die elektriese stroom van die geleier afhang van sy afmetings: lengte, breedte, hoogte. En ook op sy vorm (bol, silinder) en die materiaal waaruit dit gemaak is. Dus, die formule vir weerstand, byvoorbeeld, van 'n homogene silindriese geleier sal wees: R \u003d pl / S.
As ons in hierdie formule s=1 m2 en l=1 m plaas, dan sal R numeries gelyk wees aan p. Van hier af word die maateenheid vir die weerstandskoëffisiënt van die geleier in SI bereken - dit is Ohmm.

In die weerstandsformule is p die weerstandskoëffisiënt wat bepaal word deur die chemiese eienskappe van die materiaal waaruit die geleier gemaak is.
Om die differensiële vorm van Ohm se wet te oorweeg, moet ons nog 'n paar konsepte oorweeg.
Huidige digtheid
Soos jy weet, is elektriese stroom 'n streng geordende beweging van enige gelaaide deeltjies. Byvoorbeeld, in metale is stroomdraers elektrone, en in geleidende gasse ione.
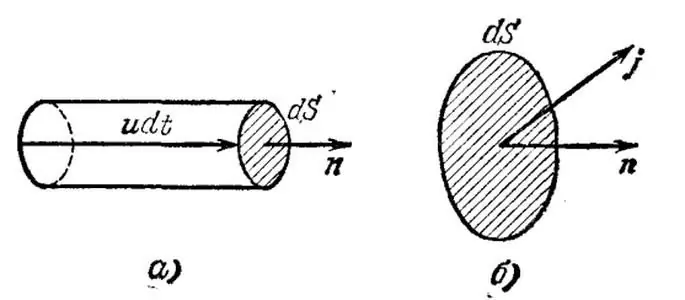
Neem die onbenullige saak wanneer alle huidige draershomogeen - metaal geleier. Laat ons verstandelik 'n oneindig klein volume in hierdie geleier uitsonder en met u die gemiddelde (dryf, geordende) snelheid van elektrone in die gegewe volume aandui. Laat n verder die konsentrasie stroomdraers per eenheidsvolume aandui.
Kom ons teken nou 'n oneindige oppervlakte dS loodreg op die vektor u en bou langs die snelheid 'n oneindige silinder met 'n hoogte udt, waar dt die tyd aandui waartydens alle stroomsnelheidsdraers wat in die geagte volume vervat is, sal verbygaan deur die area dS.
In hierdie geval sal die lading gelyk aan q=neudSdt deur elektrone oorgedra word deur die area, waar e die elektronlading is. Dus, die elektriese stroomdigtheid is 'n vektor j=neu, wat die hoeveelheid lading aandui wat per eenheid tyd deur 'n eenheidsoppervlakte oorgedra word.
Een van die voordele van Ohm se Wet-differensiaaldefinisie is dat jy dikwels kan klaarkom sonder om die weerstand te bereken.
Elektriese lading. Elektriese veldsterkte
Veldsterkte saam met elektriese lading is 'n fundamentele parameter in die teorie van elektrisiteit. Terselfdertyd kan 'n kwantitatiewe idee daarvan verkry word uit eenvoudige eksperimente wat vir skoolkinders beskikbaar is.
Vir eenvoud sal ons 'n elektrostatiese veld oorweeg. Dit is 'n elektriese veld wat nie met tyd verander nie. So 'n veld kan deur stilstaande elektriese ladings geskep word.
Ook 'n toetsheffing is nodig vir ons doeleindes. In sy hoedanigheid sal ons 'n gelaaide liggaam gebruik - so klein dat dit nie in staat is om te veroorsaak nieenige versteurings (herverdeling van ladings) in die omliggende voorwerpe.
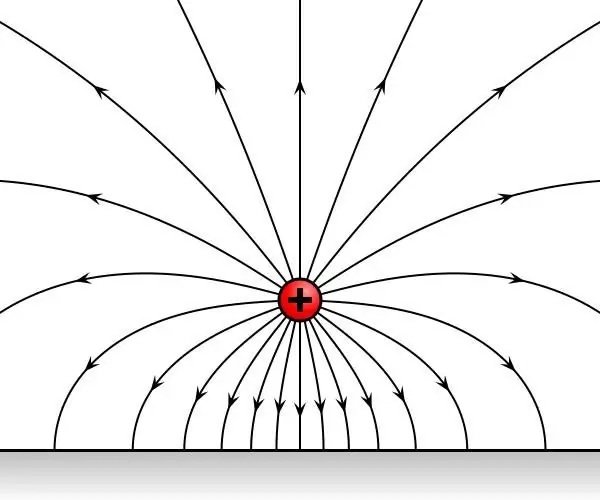
Kom ons oorweeg om die beurt twee toetsladings wat geneem is, agtereenvolgens op een punt in die ruimte geplaas, wat onder die invloed van 'n elektrostatiese veld is. Dit blyk dat die aanklagte aan tydonveranderlike invloed van sy kant onderwerp sal word. Laat F1 en F2 die kragte wees wat op die aanklagte inwerk.
As gevolg van die veralgemening van eksperimentele data, is gevind dat die kragte F1 en F2 óf in een of gerig is in teenoorgestelde rigtings, en die verhouding F1/F2 is onafhanklik van die punt in die ruimte waar die toetsladings afwisselend geplaas is. Daarom is die verhouding F1/F2 'n kenmerk van die ladings self, en hang nie van die veld af nie.
Die ontdekking van hierdie feit het dit moontlik gemaak om die elektrisasie van liggame te karakteriseer en is later elektriese lading genoem. Dus, per definisie, blyk dit q1/q2=F1/F 2 , waar q1 en q2 - die hoeveelheid heffings wat by een punt van die veld geplaas is, en F 1 en F2 - kragte wat op aanklagte van die kant van die veld inwerk.
Uit sulke oorwegings is die groottes van die ladings van verskeie deeltjies eksperimenteel vasgestel. Deur voorwaardelik een van die toetsladings gelyk aan een in die verhouding te stel, kan jy die waarde van die ander lading bereken deur die verhouding F1/F2 te meet.
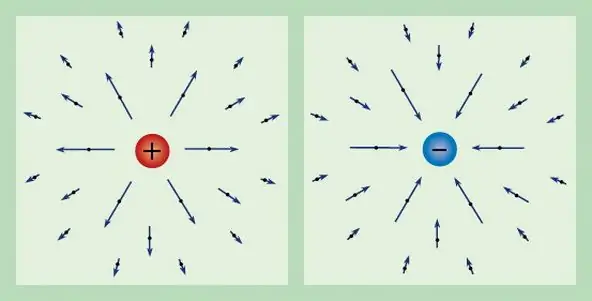
Enige elektriese veld kan gekenmerk word deur 'n bekende lading. Die krag wat dus in rus op 'n eenheidstoetslading inwerk, word die elektriese veldsterkte genoem en word deur E aangedui. Uit die definisie van die lading kry ons dat die sterktevektor die volgende vorm het: E=F/q.
Verbinding van vektore j en E. Nog 'n vorm van Ohm se wet
In 'n homogene geleier sal die geordende beweging van gelaaide deeltjies in die rigting van die vektor E plaasvind. Dit beteken dat die vektore j en E saamgerig sal wees. Soos in die bepaling van die stroomdigtheid, kies ons 'n oneindig klein silindriese volume in die geleier. Dan sal 'n stroom gelyk aan jdS deur die dwarssnit van hierdie silinder gaan, en die spanning wat op die silinder aangelê word, sal gelyk wees aan Edl. Die formule vir die weerstand van 'n silinder is ook bekend.
Dan, deur die formule vir die stroomsterkte op twee maniere te skryf, kry ons: j=E/p, waar die waarde 1/p elektriese geleiding genoem word en die inverse van elektriese weerstand is. Dit word gewoonlik as σ (sigma) of λ (lambda) aangedui. Die eenheid van geleidingsvermoë is Sm/m, waar Sm Siemens is. Eenheid inverse van Ohm.
Ons kan dus die vraag hierbo oor Ohm se wet vir 'n onhomogene stroombaan beantwoord. In hierdie geval sal die stroomdraers beïnvloed word deur die krag van die elektrostatiese veld, wat gekenmerk word deur die intensiteit E1, en ander kragte wat op hulle inwerk vanaf 'n ander stroombron, wat kan wees aangewys E 2. Toe het Ohm se wet gegeldinhomogene gedeelte van die ketting sal soos volg lyk: j=λ(E1 + E2).
Meer oor geleidingsvermoë en weerstand
Die vermoë van 'n geleier om 'n elektriese stroom te gelei word gekenmerk deur sy weerstand, wat gevind kan word deur die weerstandsformule, of geleiding, bereken as die wederkerige van geleidingsvermoë. Die waarde van hierdie parameters word bepaal deur beide die chemiese eienskappe van die geleiermateriaal en deur eksterne toestande. Veral die omgewingstemperatuur.
Vir die meeste metale is die weerstand by normale temperatuur eweredig daaraan, dit wil sê p ~ T. Afwykings word egter by lae temperature waargeneem. Vir 'n groot aantal metale en legerings by temperature naby aan 0°K, het die weerstandsberekening nulwaardes getoon. Hierdie verskynsel word supergeleiding genoem. Byvoorbeeld, kwik, tin, lood, aluminium, ens. het hierdie eienskap. Elke metaal het sy eie kritieke temperatuur Tk, waarby die verskynsel van supergeleiding waargeneem word.
Neem ook kennis dat die definisie van silinderweerstand veralgemeen kan word na drade wat van dieselfde materiaal gemaak is. In hierdie geval sal die deursnee-area van die weerstandsformule gelyk wees aan die dwarssnit van die draad, en l - sy lengte.






