In termodinamika, wanneer oorgange van die aanvanklike tot die finale toestand van 'n sisteem bestudeer word, is dit belangrik om die termiese effek van die proses te ken. Die konsep van hittekapasiteit is nou verwant aan hierdie effek. In hierdie artikel sal ons die vraag oorweeg wat bedoel word met die isochoriese hittekapasiteit van 'n gas.
Ideale gas
'n Ideale gas is 'n gas waarvan die deeltjies as materiële punte beskou word, dit wil sê hulle het nie afmetings nie, maar het massa, en waarin alle interne energie uitsluitlik bestaan uit die kinetiese energie van die beweging van molekules en atome.
Enige werklike gas sal ideaal nooit aan die beskryfde model voldoen nie, aangesien sy deeltjies steeds 'n paar lineêre afmetings het en met mekaar in wisselwerking tree deur swak Van der Waals-bindings of chemiese bindings van 'n ander tipe. By lae druk en hoë temperature is die afstande tussen molekules egter groot, en hul kinetiese energie oorskry die potensiële energie met dosyne kere. Dit alles maak dit moontlik om met 'n hoë mate van akkuraatheid die ideale model vir regte gasse toe te pas.
Interne energie van gas
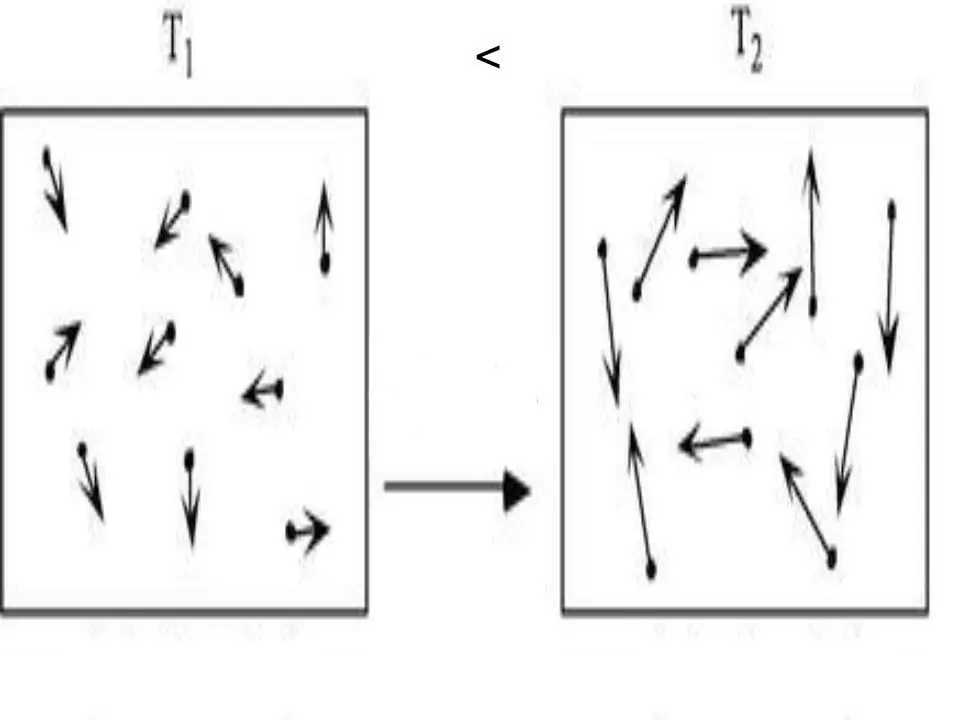
Die interne energie van enige stelsel is 'n fisiese eienskap, wat gelyk is aan die som van potensiële en kinetiese energie. Aangesien potensiële energie in ideale gasse verwaarloos kan word, kan ons die gelykheid daarvoor skryf:
U=Ek.
Waar Ek die energie van die kinetiese sisteem is. Deur die molekulêre kinetiese teorie te gebruik en die universele Clapeyron-Mendeleev-toestandsvergelyking toe te pas, is dit nie moeilik om 'n uitdrukking vir U te verkry nie. Dit word hieronder geskryf:
U=z/2nRT.
Hier is T, R en n onderskeidelik die absolute temperatuur, die gaskonstante en die hoeveelheid stof. Die z-waarde is 'n heelgetal wat die aantal vryheidsgrade aandui wat 'n gasmolekule het.
Isobariese en isochoriese hittekapasiteit
In fisika is hittekapasiteit die hoeveelheid hitte wat aan die sisteem wat bestudeer word verskaf moet word om dit met een kelvin te verhit. Die omgekeerde definisie is ook waar, dit wil sê, die hittekapasiteit is die hoeveelheid hitte wat die stelsel vrystel wanneer dit met een kelvin afgekoel word.
Die maklikste manier vir 'n stelsel is om die isochoriese hittekapasiteit te bepaal. Dit word verstaan as die hittekapasiteit by konstante volume. Aangesien die stelsel nie werk onder sulke toestande verrig nie, word alle energie bestee aan die verhoging van interne energiereserwes. Kom ons dui die isochoriese hittekapasiteit aan met die simbool CV, dan kan ons skryf:
dU=CVdT.
Dit is die verandering in interne energiestelsel is direk eweredig aan die verandering in sy temperatuur. As ons hierdie uitdrukking vergelyk met die gelykheid wat in die vorige paragraaf geskryf is, kom ons by die formule vir CV in 'n ideale gas:
СV=z/2nR.
Hierdie waarde is ongerieflik om in die praktyk te gebruik, aangesien dit afhang van die hoeveelheid stof in die stelsel. Daarom is die konsep van spesifieke isochoriese hittekapasiteit bekendgestel, dit wil sê 'n waarde wat óf per 1 mol gas óf per 1 kg bereken word. Kom ons dui die eerste waarde aan met die simbool CV, die tweede - met die simbool CV m. Vir hulle kan jy die volgende formules skryf:
CV=z/2R;
CVm=z/2R/M.
Hier is M die molêre massa.
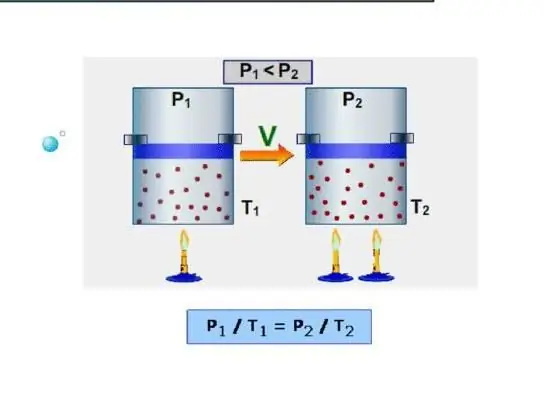
Isobaars is die hittekapasiteit terwyl 'n konstante druk in die stelsel gehandhaaf word. 'n Voorbeeld van so 'n proses is die uitsetting van gas in 'n silinder onder 'n suier wanneer dit verhit word. Anders as die isochoriese proses, word die hitte wat aan die sisteem voorsien word, tydens die isobariese proses bestee om die interne energie te verhoog en om meganiese werk te verrig, dit wil sê:
H=dU + PdV.
Die entalpie van 'n isobariese proses is die produk van die isobariese hittekapasiteit en die verandering in temperatuur in die sisteem, dit is:
H=CPdT.
As ons die uitsetting by 'n konstante druk van 1 mol gas oorweeg, dan sal die eerste wet van termodinamika geskryf word as:
CPdT=CV dT + RdT.
Die laaste term word uit die vergelyking verkryClapeyron-Mendeleev. Uit hierdie gelykheid volg die verband tussen isobariese en isochoriese hittekapasiteite:
CP=CV + R.
Vir 'n ideale gas is die spesifieke molêre hittekapasiteit by konstante druk altyd groter as die ooreenstemmende isochoriese eienskap met R=8, 314 J/(molK).
Grade van vryheid van molekules en hittekapasiteit
Kom ons skryf weer die formule vir die spesifieke molêre isochoriese hittekapasiteit:
CV=z/2R.
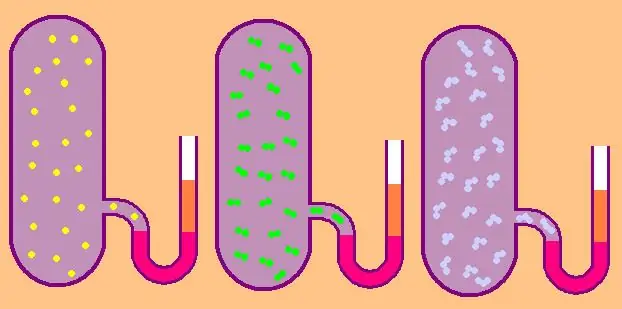
In die geval van 'n monatomiese gas is die waarde z=3, aangesien atome in die ruimte slegs in drie onafhanklike rigtings kan beweeg.
As ons praat van 'n gas wat uit diatomiese molekules bestaan, byvoorbeeld, suurstof O2 of waterstof H2, dan, benewens translasiebeweging, kan hierdie molekules steeds om twee onderling loodregte asse roteer, dit wil sê, z sal gelyk wees aan 5.
Vir meer komplekse molekules, gebruik z=6. om CV
te bepaal






