Die natuurlike verskynsels en prosesse rondom ons is redelik kompleks. Vir hul presiese fisiese beskrywing moet 'n omslagtige wiskundige apparaat gebruik word en 'n groot aantal beduidende faktore moet in ag geneem word. Om hierdie probleem te vermy, word sommige vereenvoudigde modelle in fisika gebruik, wat die wiskundige ontleding van die proses baie vergemaklik, maar feitlik nie die akkuraatheid van die beskrywing daarvan beïnvloed nie. Een daarvan is die ideale gasmodel. Kom ons oorweeg dit in meer besonderhede in die artikel.
Die konsep van 'n ideale gas
'n Ideale gas is 'n toestand van samevoeging van 'n stof, wat bestaan uit materiële punte wat nie met mekaar in wisselwerking is nie. Kom ons verduidelik hierdie definisie in meer besonderhede.
Eers praat ons van materiële punte as voorwerpe wat 'n ideale gas vorm. Dit beteken dat sy molekules en atome nie 'n grootte het nie, maar 'n sekere massa. Dit is vet'n benadering kan gemaak word met inagneming van die feit dat in alle werklike gasse by lae druk en hoë temperature, die afstand tussen molekules baie groter is as hul lineêre afmetings.
Tweedens, die molekules in 'n ideale gas behoort nie met mekaar te reageer nie. In werklikheid bestaan sulke interaksies altyd. Dus, selfs atome van edelgasse ervaar dipool-dipool-aantrekking. Met ander woorde, Van der Waals-interaksies is aanwesig. In vergelyking met die kinetiese energie van rotasie en translasiebeweging van molekules, is hierdie interaksies egter so klein dat dit nie die eienskappe van gasse beïnvloed nie. Daarom kan hulle nie in ag geneem word wanneer praktiese probleme opgelos word nie.
Dit is belangrik om daarop te let dat nie alle gasse waarin die digtheid laag is en die temperatuur hoog is, as ideaal beskou kan word nie. Benewens Van der Waals-interaksies is daar ander, sterker tipes bindings, byvoorbeeld waterstofbindings tussen H2O-molekules, wat lei tot 'n growwe skending van die gas-idealiteitsvoorwaardes. Om hierdie rede is waterdamp nie 'n ideale gas nie, maar lug wel.
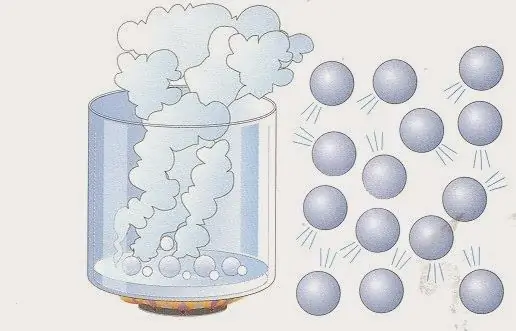
Fisiese model van 'n ideale gas
Hierdie model kan soos volg voorgestel word: veronderstel dat die gasstelsel N-deeltjies bevat. Dit kan atome en molekules van verskeie chemikalieë en elemente wees. Die aantal N deeltjies is groot, so die eenheid "mol" word gewoonlik gebruik om dit te beskryf (1 mol stem ooreen met Avogadro se getal). Hulle beweeg almal in een of ander volume V. Deeltjiebewegingsis chaoties en onafhanklik van mekaar. Elkeen van hulle het 'n sekere spoed v en beweeg langs 'n reguit pad.
Teoreties is die waarskynlikheid van botsing tussen partikels byna nul, aangesien hul grootte klein is in vergelyking met die interpartikelafstande. As so 'n botsing egter plaasvind, is dit absoluut elasties. In laasgenoemde geval bly die totale momentum van die deeltjies en hul kinetiese energie behoue.
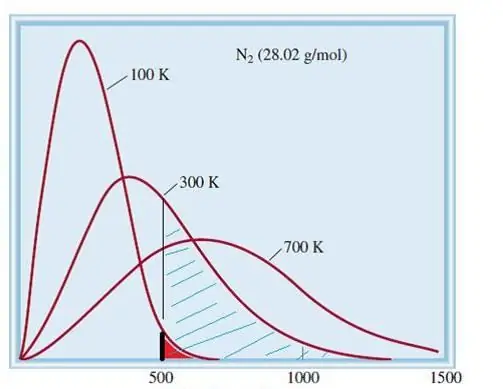
Die oorwoë model van ideale gasse is 'n klassieke stelsel met 'n groot aantal elemente. Daarom gehoorsaam die spoed en energie van deeltjies daarin die statistiese verspreiding van Maxwell-Boltzmann. Sommige deeltjies het lae snelhede, terwyl ander hoë snelhede het. In hierdie geval is daar 'n sekere smal spoedgrens, waarin die mees waarskynlike waardes van hierdie hoeveelheid lê. Die snelheidsverspreiding van stikstofmolekules word skematies hieronder getoon.
Kinetiese teorie van gasse
Die model van ideale gasse wat hierbo beskryf word, bepaal uniek die eienskappe van gasse. Hierdie model is die eerste keer in 1738 deur Daniel Bernoulli voorgestel.

Vervolgens is dit tot sy huidige toestand ontwikkel deur August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski en ander wetenskaplikes.
Die kinetiese teorie van vloeibare stowwe, op grond waarvan die ideale gasmodel gebou word, verduidelik twee belangrike makroskopiese eienskappe van die sisteem op grond van sy mikroskopiese gedrag:
- Die druk in gasse is die gevolg van die botsing van deeltjies met die wande van die vaartuig.
- Die temperatuur in die sisteem is die resultaat van die manifestasie van die konstante beweging van molekules en atome.
Kom ons brei uit oor beide gevolgtrekkings van die kinetiese teorie.
Gasdruk
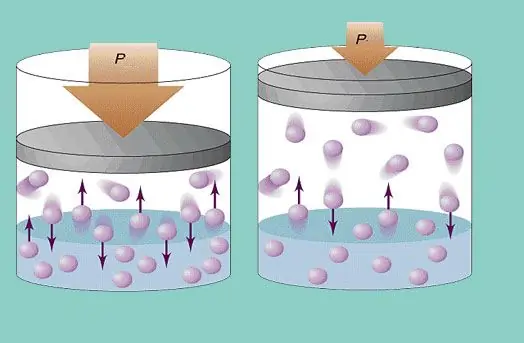
Die ideale gasmodel veronderstel 'n konstante chaotiese beweging van deeltjies in die sisteem en hul konstante botsing met die wande van die vaartuig. Elke so 'n botsing word as absoluut elasties beskou. Die deeltjiemassa is klein (≈10-27-10-25 kg). Daarom kan dit nie baie druk in 'n botsing skep nie. Nietemin is die aantal deeltjies, en dus die aantal botsings, groot (≈1023). Daarbenewens is die wortel gemiddelde kwadraatsnelheid van die elemente 'n paar honderd meter per sekonde by kamertemperatuur. Dit alles lei tot die skepping van aansienlike druk op die mure van die vaartuig. Dit kan met die volgende formule bereken word:
P=Nmvcp2 / (3V), waar vcp wortel gemiddelde vierkantsnelheid is, m deeltjiemassa is.
Absolute temperatuur
Volgens die ideale gasmodel word die temperatuur uniek bepaal deur die gemiddelde kinetiese energie van 'n molekule of atoom in die sisteem wat bestudeer word. Jy kan die volgende uitdrukking skryf wat kinetiese energie en absolute temperatuur vir 'n ideale gas in verband bring:
mvcp2 / 2=3 / 2kB T.
Hier kB is die Boltzmann-konstante. Uit hierdie gelykheid kry ons:
T=m vcp2 / (3kB).
Universele toestandsvergelyking
As ons bogenoemde uitdrukkings vir absolute druk P en absolute temperatuur T kombineer, kan ons die volgende gelykheid skryf:
PV=nRT.
Hier is n die hoeveelheid stof in mol, R is die gaskonstante wat deur D. I. Mendeleev ingevoer word. Hierdie uitdrukking is die belangrikste vergelyking in die teorie van ideale gasse, want dit kombineer drie termodinamiese parameters (V, P, T) en is nie afhanklik van die chemiese eienskappe van die gasstelsel nie.

Die universele vergelyking is die eerste keer eksperimenteel afgelei deur die Franse fisikus Emile Clapeyron in die 19de eeu en toe tot sy moderne vorm gebring deur die Russiese chemikus Mendeleev, en dit is hoekom dit tans die name van hierdie wetenskaplikes dra.






