Belangstelling in programmering neem elke jaar toe. En as hulle in instellings wat spesialiseer in die skryf van programme op so 'n programmeertaal soos C ++ staatmaak, dan maak studente in skole en tegniese skole kennis met "Pascal". En reeds op grond van hierdie taal begin hulle programmering verstaan deur die gebruik van Delphi-sagteware. Daar moet dadelik op gelet word dat hierdie programmeertale 'n groot ruimte bied vir die manifestasie van hul verbeelding. En as jy met behulp van die Pascal-taal kennis kan maak met die basiese konsepte van programmering, dan kan jy in Delphi reeds 'n volwaardige program skryf. En nogal 'n belangrike plek in die skryf van programme word soms ingeneem deur die oplos van skikkings in "Pascal".
Die teenwoordigheid van 'n groot aantal baie verskillende veranderlikes

Daar is heelwat verskillende veranderlikes in 'n programmeertaal, wat gekenmerk word deur die teenwoordigheid van slegs een waarde. Hulle is in staat om 'n enkele waarde wat 'n sekere tipe het, te stoor. Stringveranderlikes is die uitsondering. Hulle isis 'n versameling van daardie data waarvoor die karaktertipe kenmerkend is. Maar selfs sulke veranderlikes word gewoonlik vanuit die posisie van 'n aparte waarde beskou.
Dit is geen geheim dat jy met behulp van 'n rekenaar die tyd om sekere werk wat met groot hoeveelhede data verband hou, aansienlik kan verminder. Maar hoe, wanneer slegs daardie veranderlikes gebruik word wat tipes het wat aan mense bekend is, is dit moontlik om die resultate van werk in die geheue te stoor, en ook daardie data te verwerk wat 'n groot aantal rye bevat? Sulke take is redelik algemeen in enige aktiwiteitsveld.
Natuurlik kan jy altyd soveel veranderlikes invoer as wat jy nodig het om jou doelwitte te bereik. U kan ook sekere waardes daarvoor definieer. Maar die kode van die program sal net hieruit toeneem. Dit is moeilik om die kode wat 'n groot aantal reëls het, te lees. Veral wanneer dit nodig is om foute te vind.
Gevolglik het die programmeerders oor hierdie vraag gedink. Dit is hoekom die tale wat tot dusver ontwikkel is, sulke veranderlikes het wat dit moontlik maak om 'n groot hoeveelheid data in hulself te stoor. Die skikking in "Pascal" het baie verander in die benadering tot programmering. Daarom word dit as 'n belangrike veranderlike in 'n programmeertaal beskou.
Die gebruik van skikkings kan kodegrootte drasties verminder
Onder hierdie term is 'n geordende reeks data versteek, wat deur een tipe gekenmerk word. Daarbenewens kry al hierdie data dieselfde naam. Dit behoort ookDaar moet kennis geneem word dat baie voorwerpe van die werklike wêreld hierdie definisie kan pas: woordeboeke, spotprente en nog baie meer. Die maklikste manier om 'n skikking in "Pascal" aan te bied, is egter in die vorm van 'n soort tabel. Elke individuele sel bevat een veranderlike. Deur koördinate te gebruik, kan jy die posisie van die veranderlike wat dit in die algemene tabel sal beklee bepaal.
Wat beteken 'n eendimensionele skikking?
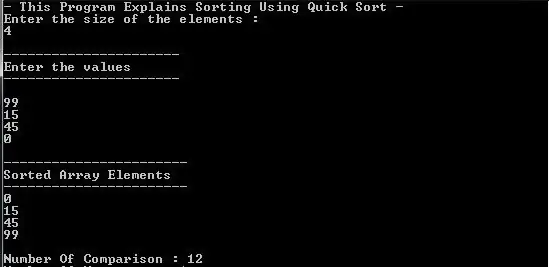
Die eenvoudigste tabel is die een wat lineêr is. In hierdie skikking, om die ligging van die parameter te bepaal, is dit genoeg om slegs een nommer te spesifiseer. Meer komplekse skikkings word op grond daarvan gevorm.
Om eendimensionele skikkings in "Pascal" te beskryf, voer net die volgende kode in: Tik Array of.
Die getalle is daardie veranderlikes wat 'n ordinale tipe kan hê. Wanneer 'n reeks gespesifiseer word, is dit die moeite werd om te verstaan dat die aanvanklike getal nie hoër as die finale een kan wees nie. Die tipe wat die skikking elemente het, kan absoluut enigiets wees - hetsy standaard of reeds voorheen beskryf. Die keuse sal afhang van die behoefte om 'n spesifieke probleem op te los.
Hoe word 'n lineêre skikking beskryf?
Dit is moontlik om onmiddellik eendimensionele skikkings in "Pascal" te beskryf. Dit moet in 'n spesiale afdeling gedoen word, wat nodig is vir hierdie spesifieke prosedure. Jy sal die volgende kode moet invoer: Var: Skikking Van.
Om te verstaan hoe jy 'n skikking in Pascal kan beskryf, moet jy die volgende kode invoer:
- Var
- S, VV: Array[5..50] Of Real;
- K: Skikking['C'.. 'R'] van heelgetal;
- Z: Skikking [-10..10] Woord;
- E: Skikking [3..30] Van Real.
In hierdie voorbeeld is die veranderlikes S, VV en T 'n skikking van daardie getalle wat reëel is. Die veranderlike K verberg die karaktertipe en daardie elemente. Wat heelgetalle is. Die Z-skikking stoor nommers waarvan die tipe Word is.
Tussen al die aksies wat gebruik kan word wanneer met 'n skikking gewerk word, kan opdrag onderskei word. Die hele tafel kan daaraan onderwerp word. Byvoorbeeld, S:=VV. Maar dit moet verstaan word dat opdragbewerkings slegs aan 'n skikking in "Pascal" onderwerp kan word wat 'n sekere tipe het.
Daar is nie meer bewerkings wat op die hele skikking gelyktydig uitgevoer kan word nie. Jy kan egter op dieselfde manier met elemente werk as met ander priemgetalle wat 'n sekere tipe het. Om na 'n individuele parameter te verwys, moet jy die naam van die skikking spesifiseer. Deur vierkantige hakies te gebruik, moet jy die indeks bepaal wat kenmerkend is van die verlangde element. Byvoorbeeld: K[12].
Belangrikste verskille tussen skikkings en ander veranderlikes
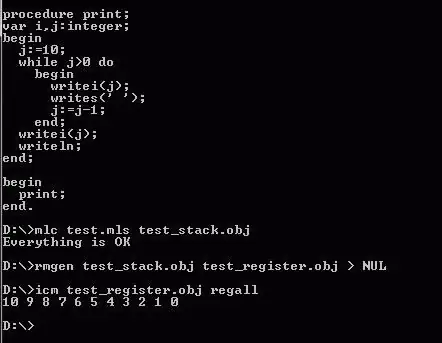
Die basiese verskil tussen tabelkomponente en eenvoudige veranderlikes is dat dit moontlik is om nie net die indekswaarde tussen hakies te plaas nie, maar ook so 'n uitdrukking wat tot die verlangde waarde kan lei. 'n Voorbeeld van indirekte adressering kan wees: V[K]. In hierdie geval neem die veranderlike K 'n sekere waarde aan. Van hierdiedit volg dat jy 'n lus kan gebruik wanneer jy 'n skikking vul, verwerk en druk.
Hierdie vorm van organisasie kan voorkom in die geval van stringveranderlikes wat naby genoeg in hul eienskappe aan skikkings van tipe Char is. Maar daar is ook verskille. Hulle is soos volg:
- Stringveranderlikes kan altyd vanaf die sleutelbord ingevoer en op die skerm gedruk word.
- String veranderlikes is beperk in lengte. Jy kan 'n maksimum van 255 karakters invoer. Die kritieke grootte van die skikking is 64 kb.
Watter metodes kan gebruik word om skikkingsdata op die skerm te vertoon?
Jy moet let op die manier waarop die inhoud van die skikking vertoon word. Daar is verskeie.
- Writeln (A[1], A[2], A[3]). So 'n voorbeeld, hoewel primitief, is in staat om te wys hoe jy direk toegang tot elke individuele element inherent in die tabel kan verkry. Sommige van die voordele wat Pascal-skikkings bo eenvoudige veranderlikes het, is egter nie hier sigbaar nie.
-
Program A1;
Var B: Skikking [1..10] Van Heelgetal;
K: Heelgetal;
Begin
Vir K:=1 Tot 10 Doen {Hierdie opdrag loop met parameter }
Readln(A[K]); {A[I] word ingevoer met die sleutelbord }
Vir K:=10 Af tot 1 Doen {Die tabel word in omgekeerde volgorde gedruk}
Skryf(A[K], 'VVV') Einde.
'n Soortgelyke kode van die program vir skikkings in "Pascal" demonstreer hoe jy 10 nommers met die sleutelbord kan invoer, dit uitdruk, en die waardes in omgekeerde volgorde herrangskik. As dieselfde program herskryf word vanafdie gebruik van 'n groot aantal veranderlikes in plaas van 'n skikking, dan sal die kode aansienlik verhoog word. En dit bemoeilik die proses om die program te lees baie.
Toename in moontlikhede deur die gebruik van skikkings

Dit is ook moontlik om tabelle te vul met waardes wat gelyk is aan die kwadraat van elementindekse. Dit is ook moontlik om so 'n reeks stringe in "Pascal" te skep, wat sal toelaat dat alle getalle outomaties ingevoer word. Soos jy kan sien, verbeter die gebruik van 'n skikking die vermoëns van die Pascal-programmeertaal aansienlik.
Verwerking van lineêre skikkings is baie algemeen in verskeie take. Daarom is daar niks vreemd in die feit dat hulle in institute en skole bestudeer word nie. Boonop is die moontlikhede wat skikkings dra redelik uitgebreid.
Wat is versteek onder tweedimensionele skikkings?
Jy kan jou 'n tabel voorstel wat uit verskeie rye gelyktydig bestaan. Elke individuele ry bevat verskeie selle. In so 'n situasie, om die posisie van die selle akkuraat te bepaal, is dit nodig om nie een indeks te merk nie, soos die geval was met lineêre skikkings, maar twee - getalle wat kenmerkend is van 'n ry en 'n kolom. Tweedimensionele skikkings in "Pascal" word gekenmerk deur 'n soortgelyke voorstelling.
Hoe om tabelle van hierdie soort te beskryf?
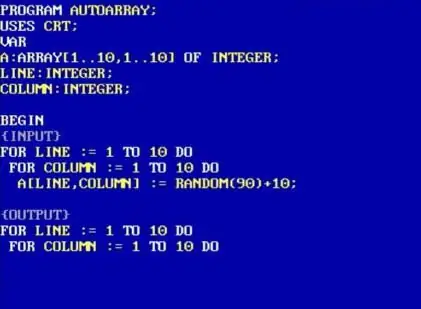
Die datastruktuur wat in die Pascal-taal gevind word om die waardes van so 'n tabel te stoor, isdie naam van 'n tweedimensionele skikking. Beskrywing van so 'n skikking is onmiddellik moontlik deur twee metodes te gebruik.
- Var B: Skikking[1..15] Van Skikking [1..30] Van Heelgetal;
- Var B: Skikking [1..15, 1..30] van heelgetal.
In al hierdie gevalle word 'n tweedimensionele skikking beskryf, wat 15 rye en 30 kolomme het. Die beskrywings wat hierbo gegee is, is absoluut ekwivalent. Om met enige van die elemente te begin werk, is dit nodig om twee indekse toe te ken. Byvoorbeeld, A[6][5] of A[6, 5].
Die uitset na die skerm sal amper dieselfde wees as in die geval van 'n eendimensionele skikking. Jy hoef net twee indekse te spesifiseer. In alle ander opsigte is daar geen verskille as sodanig nie, so dit is nie nodig om lank daaroor te praat nie.
Eerste manier om te sorteer
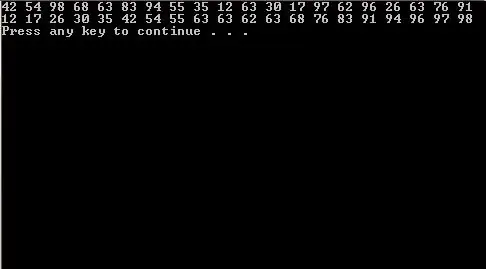
Soms word dit nodig om data te sorteer. Hiervoor het die taal ooreenstemmende opdragte. Daar is twee algoritmes waarmee 'n skikking in Pascal gesorteer kan word. Die betekenis van die direkte seleksiemetode lê in die feit dat deur die nes van die lus, absoluut elke tabelveranderlike met ander waardes vergelyk sal word. Met ander woorde, as daar 'n skikking van 15 getalle is, sal eerste nommer 1 met ander getalle vergelyk word. Dit sal gebeur totdat byvoorbeeld die element wat groter is as die eerste getal gevind word. Vervolgens sal die vergelyking presies hierdie syfer plaasvind. Dit sal herhaal word totdat die grootste gevind word.element van alle voorgestelde. Hierdie metode is redelik eenvoudig vir daardie programmeerders wat pas in die taal begin werk het.
Tweede skikking sorteermetode
Die tweede manier is borrel. Die kern van hierdie tegniek lê in die feit dat naburige elemente in pare vergelyk word. Byvoorbeeld, 1 en 2, 2 en 3, 3 en 4, ens. In die geval dat die gevonde waarde ten volle aan die sorteervoorwaardes voldoen, sal dit na die einde van die hele skikking geskuif word, dit wil sê dit sal verskyn as 'n "borrel". Hierdie algoritme is die moeilikste om te onthou. Jy hoef dit egter nie te slyp nie. Die belangrikste ding is om die hele struktuur van die kode te verstaan. En slegs in hierdie geval kan 'n mens daarop aanspraak maak om groot hoogtes in programmering te bereik.
Gevolgtrekking

Ons hoop jy verstaan wat skikkings is en hoe jy kan sorteer om 'n spesifieke waarde te vind of 'n spesifieke doelwit te bereik. As jy "Pascal" gekies het om 'n spesifieke probleem op te los, waarin skikkings 'n belangrike plek inneem, dan sal jy hul studie deeglik moet benader. Dit word beïnvloed deur so 'n faktor soos die teenwoordigheid in die taal van 'n voldoende groot aantal veranderlikes wat in sekere situasies gebruik word om die hele kode as 'n geheel te vereenvoudig. Skikkings word met reg as die hoofhoeveelhede beskou, waarvan die studie sonder versuim moet plaasvind.






