Daar is voorwerpe wat in staat is om die digtheid van die elektromagnetiese stralingsvloed wat op hulle val, te verander, dit wil sê, dit óf te verhoog deur dit op een punt te versamel, óf dit te verminder deur dit te verstrooi. Hierdie voorwerpe word in fisika lense genoem. Kom ons bekyk hierdie kwessie van naderby.
Wat is lense in fisika?
Hierdie konsep beteken absoluut enige voorwerp wat in staat is om die voortplantingsrigting van elektromagnetiese straling te verander. Dit is die algemene definisie van lense in fisika, wat optiese brille, magnetiese en gravitasielense insluit.
In hierdie artikel sal die fokus wees op optiese bril, wat voorwerpe is wat van 'n deursigtige materiaal gemaak word en deur twee oppervlaktes beperk word. Een van hierdie oppervlaktes moet noodwendig kromming hê (dit wil sê, deel wees van 'n sfeer met eindige radius), anders sal die voorwerp nie die eienskap hê om die voortplantingsrigting van ligstrale te verander nie.
Die beginsel van die lens

Die kern van die werk van hierdie ongekompliseerdeoptiese voorwerp is die verskynsel van breking van die son se strale. Aan die begin van die 17de eeu het die bekende Nederlandse fisikus en sterrekundige Willebrord Snell van Rooyen die wet van breking gepubliseer, wat tans sy van dra. Die formulering van hierdie wet is soos volg: wanneer sonlig deur die raakvlak tussen twee opties deursigtige media beweeg, dan is die produk van die sinus van die invalshoek tussen die straal en die normaal op die oppervlak en die brekingsindeks van die medium waarin dit versprei is 'n konstante waarde.

Om bogenoemde te verduidelik, kom ons gee 'n voorbeeld: laat die lig op die oppervlak van die water val, terwyl die hoek tussen die normaal tot die oppervlak en die straal θ1 is. Dan word die ligstraal gebreek en begin sy voortplanting in die water reeds teen 'n hoek θ2 met die normaal tot die oppervlak. Volgens Snell se wet kry ons: sin(θ1)n1=sonde(θ2) n2, waar n1 en n2 die brekingsindekse vir lug en water is, onderskeidelik. Wat is die brekingsindeks? Dit is 'n waarde wat wys hoeveel keer die voortplantingsspoed van elektromagnetiese golwe in vakuum groter is as dié vir 'n opties deursigtige medium, dit wil sê n=c/v, waar c en v die spoed van lig in vakuum en in die medium, onderskeidelik.
Die fisika van die voorkoms van breking lê in die implementering van Fermat se beginsel, waarvolgens lig op so 'n manier beweeg dat dit die afstand van een punt na 'n ander in die ruimte in die kortste tyd oorkom.
Tipe lense

Die tipe optiese lens in fisika word uitsluitlik bepaal deur die vorm van die oppervlaktes wat dit vorm. Die brekingsrigting van die bundel wat op hulle inval, hang af van hierdie vorm. Dus, as die kromming van die oppervlak positief (konveks) is, sal die ligstraal, wanneer dit die lens verlaat, nader aan sy optiese as voortplant (sien hieronder). Omgekeerd, as die kromming van die oppervlak negatief (konkaaf) is, en dan deur die optiese glas gaan, sal die balk wegbeweeg van sy sentrale as.
Let weer daarop dat 'n oppervlak van enige kromming strale op dieselfde manier breek (volgens Stella se wet), maar die normale daarvan het 'n ander helling relatief tot die optiese as, wat lei tot verskillende gedrag van die gebreekte straal.
'n Lens wat deur twee konvekse oppervlaktes begrens word, word 'n konvergerende lens genoem. Op sy beurt, as dit gevorm word deur twee oppervlaktes met negatiewe kromming, word dit verstrooiing genoem. Alle ander soorte optiese brille word geassosieer met 'n kombinasie van hierdie oppervlaktes, waarby 'n vlak ook gevoeg word. Watter eienskap die gekombineerde lens sal hê (divergerend of konvergerend) hang af van die totale kromming van die radiusse van sy oppervlaktes.
Lenselemente en straleienskappe

Om lense in beeldfisika in te bou, moet jy vertroud raak met die elemente van hierdie voorwerp. Hulle word hieronder gelys:
- Hoofoptiese as en middelpunt. In die eerste geval beteken hulle 'n reguit lyn wat loodreg op die lens deur sy optiese middelpunt gaan. Laasgenoemde is op sy beurt 'n punt binne die lens, wat deurgaan waardeur die straal nie breking ervaar nie.
- Brandpuntsafstand en fokus - die afstand tussen die middelpunt en 'n punt op die optiese as, wat al die strale wat op die lens inval parallel met hierdie as versamel. Hierdie definisie is waar vir die versameling van optiese bril. In die geval van divergente lense is dit nie die strale self wat na 'n punt sal konvergeer nie, maar hul denkbeeldige voortsetting. Hierdie punt word die hooffokus genoem.
- Optiese krag. Dit is die naam van die wederkerige van die brandpunt, dit wil sê, D \u003d 1 / f. Dit word gemeet in dioptrie (dioptrie), dit wil sê, 1 dioptrie.=1 m-1.
Die volgende is die hoofeienskappe van die strale wat deur die lens gaan:
- straal wat deur die optiese sentrum gaan, verander nie sy bewegingsrigting nie;
- strale wat parallel met die optiese hoofas inval, verander hul rigting sodat hulle deur die hooffokus beweeg;
- strale wat teen enige hoek op optiese glas val, maar deur die fokus daarvan gaan, verander hul voortplantingsrigting op so 'n manier dat hulle parallel met die optiese hoofas word.
Die bogenoemde eienskappe van strale vir dun lense in fisika (soos dit genoem word, want maak nie saak watter sfere hulle gevorm word en hoe dik hulle is nie, net die optiese eienskappe van die voorwerpmateriaal) word gebruik om beelde daarin te bou.
Beelde in optiese bril: hoe om te bou?
Hieronder is 'n figuur wat die skemas vir die bou van beelde in die konvekse en konkawe lense van 'n voorwerp uiteensit(rooi pyl) afhangende van sy posisie.
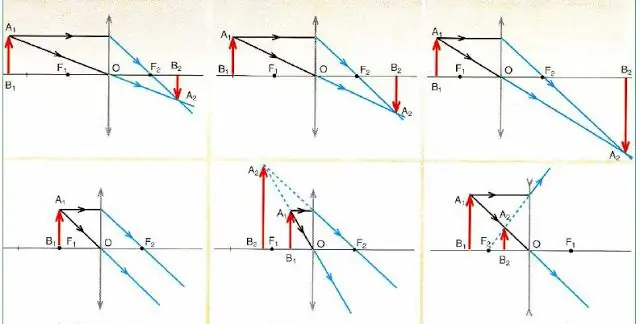
Belangrike gevolgtrekkings volg uit die ontleding van die stroombane in die figuur:
- Enige beeld is gebou op slegs 2 strale (gaan deur die middel en parallel met die optiese hoofas).
- Konvergerende lense (aangedui met pyle aan die punte wat na buite wys) kan beide 'n vergrote en verkleinde beeld gee, wat op sy beurt werklik (werklik) of denkbeeldig kan wees.
- As die voorwerp in fokus is, dan vorm die lens nie sy beeld nie (sien die onderste diagram aan die linkerkant in die figuur).
- Verstrooiende optiese bril (aangedui deur pyle aan hul punte wat na binne wys) gee altyd 'n verkleinde en virtuele beeld ongeag die posisie van die voorwerp.
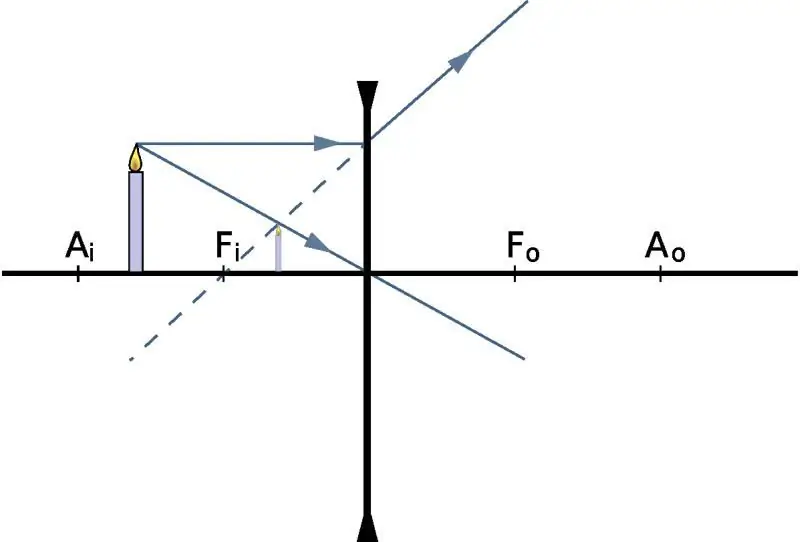
Vind die afstand na 'n prent
Om te bepaal op watter afstand die beeld sal verskyn, met kennis van die posisie van die voorwerp self, gee ons die lensformule in fisika: 1/f=1/do + 1 /d i, waar do en di die afstand na die voorwerp en na sy beeld vanaf die optiese middel, onderskeidelik, f is die hooffokus. As ons praat van 'n versamelende optiese glas, dan sal die f-nommer positief wees. Omgekeerd, vir 'n divergente lens, is f negatief.
Kom ons gebruik hierdie formule en los 'n eenvoudige probleem op: laat die voorwerp op 'n afstand do=2f van die middel van die versamelende optiese glas wees. Waar sal sy beeld verskyn?
Van die toestand van die probleem het ons: 1/f=1/(2f)+1/di. Van: 1/di=1/f - 1/(2f)=1/(2f), dit wil sê di=2 f. Die beeld sal dus op 'n afstand van twee brandpunte vanaf die lens verskyn, maar aan die ander kant as die voorwerp self (dit word aangedui deur die positiewe teken van die waarde di).
'n Kort geskiedenis
Dit is eienaardig om die etimologie van die woord "lens" te gee. Dit kom van die Latynse woorde lens en lentis, wat "lensie" beteken, aangesien optiese voorwerpe in hul vorm regtig soos die vrug van hierdie plant lyk.
Die brekingskrag van sferiese deursigtige liggame was aan die antieke Romeine bekend. Vir hierdie doel het hulle ronde glashouers gevul met water gebruik. Glaslense self het eers in die 13de eeu in Europa begin word. Hulle is gebruik as 'n leeshulpmiddel (moderne bril of 'n vergrootglas).
Die aktiewe gebruik van optiese voorwerpe in die vervaardiging van teleskope en mikroskope dateer uit die 17de eeu (aan die begin van hierdie eeu het Galileo die eerste teleskoop uitgevind). Let daarop dat die wiskundige formulering van Stella se brekingswet, sonder kennis waarvan dit onmoontlik is om lense met gewenste eienskappe te vervaardig, aan die begin van dieselfde 17de eeu deur 'n Nederlandse wetenskaplike gepubliseer is.
Ander lense
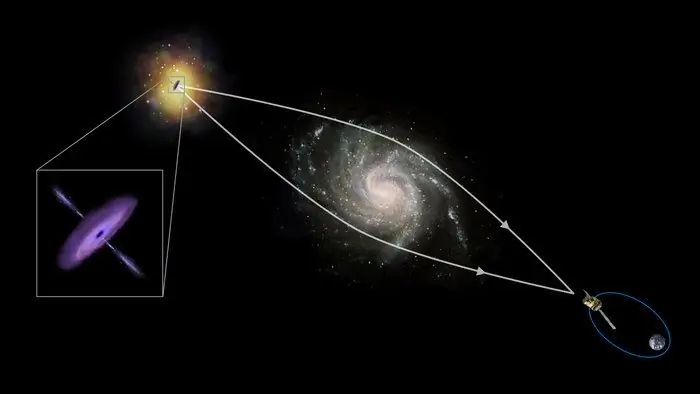
Soos hierbo genoem, is daar benewens optiese refraktiewe voorwerpe ook magnetiese en gravitasievoorwerpe. 'n Voorbeeld van eersgenoemde is magnetiese lense in 'n elektronmikroskoop, 'n aanskoulike voorbeeld van laasgenoemde is die vervorming van die rigting van die ligvloei,wanneer dit naby massiewe ruimteliggame (sterre, planete) verbygaan.






