Wanneer jy fisika in graad 10 studeer, word die onderwerp van dipole oorweeg. Wat beteken hierdie konsep en watter formules word gebruik om dit te bereken?
Inleiding
As jy 'n dipool in die ruimte van 'n eenvormige elektriese veld plaas, kan jy dit as kraglyne voorstel. 'n Dipool is 'n stelsel waarin daar twee ladings is wat identies is in parameters, maar dit is teenoorgestelde puntladings. Boonop sal die afstand tussen hulle baie minder wees as die afstand na enige punt van die dipoolveld. Die konsep van die dipoolmoment word in die skoolkursus van elektrodinamika (Graad 10) bestudeer.
Die as van die dipool is 'n reguit lyn wat deur die punte van albei ladings gaan. 'n Dipoolarm is 'n vektor wat 'n lading verbind en terselfdertyd van negatief gelaaide deeltjies na positief gelaaide deeltjies gaan. 'n Elektriese dipool word gekenmerk deur die teenwoordigheid van so 'n toestand soos 'n dipool of elektriese moment.
Per definisie is 'n dipoolmoment 'n vektor wat numeries gelyk is aan die produk van die dipoollading en sy arm. Boonop word dit saam met die skouer van die dipool gerig. By nul-gelykheid van die som van kragte, bereken ons die waarde van die moment. Vir die hoek wat bestaan tussen die dipoolmoment enrigting van die elektriese veld, die teenwoordigheid van 'n meganiese moment is kenmerkend.
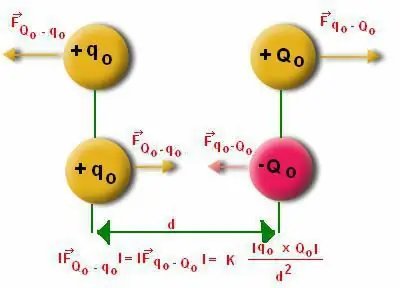
Dikwels vind mense dit moeilik om die modulus wat op die dipoolstruktuur inwerk, te bereken. Hier is dit nodig om die eienaardighede van die berekening van die hoek "Alfa" in ag te neem. Dit is bekend dat die dipool van die gebalanseerde posisie afwyk. Maar die dipoolmoment self het 'n herstellende karakter, aangesien dit geneig is om in beweging te wees.
Berekeninge
Wanneer hierdie dipoolmoment in die medium van 'n inhomogene elektriese veld geplaas word, ontstaan 'n krag onvermydelik. In so 'n omgewing sal die aanwysers van die som van kragte nie nul wees nie. Gevolglik is daar kragte wat op die dipoolmoment inwerk met 'n puntkarakter. Die grootte van die dipoolarm is baie kleiner.
Die formule kan soos volg geskryf word: F=q (E2 - E1)=qdE, waar d die elektriese velddifferensiaal is.
Soek na die kenmerke van die fisiese konsep wat bestudeer word
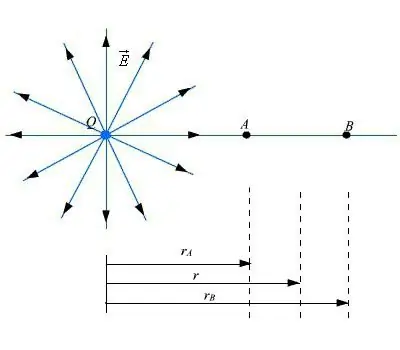
Kom ons kyk verder na die onderwerp. Om te bepaal wat die kenmerk van die elektriese veld is, as dit met behulp van 'n stelsel van ladings geskep word en in 'n klein spasie gelokaliseer word, is dit nodig om 'n aantal berekeninge te maak. 'n Voorbeeld word aangebied deur atome en molekules, wat in hul samestelling elektries gelaaide kerne en elektrone het.
As dit nodig is om te soek vir 'n veld op 'n afstand groter as die afmetings waaruit die area waar die deeltjies geleë is, sal ons 'n aantal presiese formules gebruik wat hoogs kompleks is. Dit is moontlik om eenvoudiger te gebruikbenaderde uitdrukkings. Kom ons neem aan dat puntstelle ladings qk deelneem aan die skepping van die elektriese veld. Hulle is in 'n klein spasie geleë.
Om die berekening uit te voer van die eienskap wat die veld het, word dit toegelaat om al die ladings van die stelsel te kombineer. So 'n stelsel word as 'n puntlading Q beskou. Die grootte-aanwysers sal die som wees van die ladings wat in die oorspronklike stelsel was.
Ligging van heffings
Kom ons verbeel ons dat die ligging van die lading aangedui word op enige plek waar die stelsel van ladings qk geleë is. Wanneer veranderinge aan die ligging gemaak word, as dit beperkings het wat in 'n klein area uitgedruk word, sal so 'n invloed weglaatbaar wees, byna onmerkbaar vir die veld by die oogpunt. Binne sulke grense van benadering van sterkte en potensiaal wat die elektriese veld het, word bepalings gemaak deur tradisionele formules te gebruik.
Wanneer die som van die totale lading van die stelsel nul is, sal die parameters van die aangeduide benadering rof lyk. Dit gee rede om tot die gevolgtrekking te kom dat die elektriese veld eenvoudig afwesig is. As dit nodig is om 'n meer akkurate benadering te verkry, versamel verstandelik aparte groepe positiewe en negatiewe ladings van die sisteem wat oorweeg word.
In die geval van verplasing van hul "sentrums" relatief tot ander, kan die veldparameters in so 'n stelsel beskryf word as 'n veld wat twee puntladings het, gelyk in grootte en teenoorgestelde in teken. Daar word opgemerk dat hulle verplaas word in verhouding tot ander. Om te voorsienVir 'n meer akkurate karakterisering van die stelsel van ladings in terme van die parameters van hierdie benadering, sal dit nodig wees om die eienskappe van 'n dipool in 'n elektriese veld te bestudeer.
Inleiding van die term
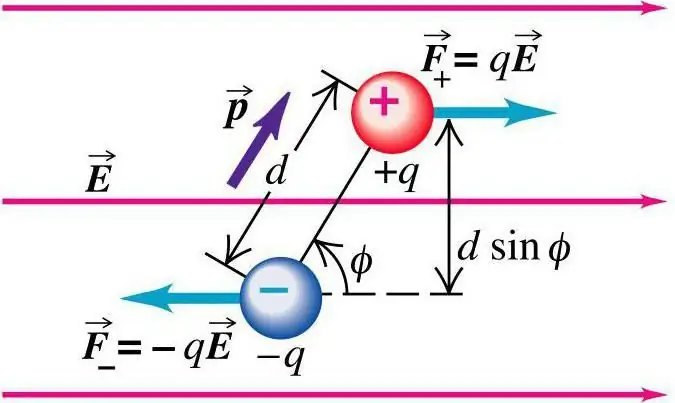
Kom ons keer terug na die definisie. 'n Elektriese dipool is die definisie van 'n stelsel wat twee puntladings het. Hulle het dieselfde grootte en teenoorgestelde tekens. Boonop is sulke tekens op klein afstande relatief tot ander tekens geleë.
Jy kan die eienskap van die proses wat deur middel van 'n dipool geskep word, bereken, en dit word voorgestel deur twee puntladings: +q en −q, en hulle is geleë op 'n afstand a relatief tot die ander.

Rekwensie van berekeninge
Kom ons begin deur die potensiaal en intensiteit te bereken wat die dipool op sy aksiale oppervlak het. Dit is 'n reguit lyn wat tussen twee ladings loop. Met dien verstande dat punt A op 'n afstand geleë is wat gelyk is aan r relatief tot die sentrale deel van die dipool, en as dit r >> a is, sal dit volgens die beginsel van superposisie vir die veldpotensiaal op hierdie punt rasionaal wees om gebruik die uitdrukking om die parameters van die elektriese dipool te bereken.
Die grootte van die sterktevektor word deur die beginsel van superposisie bereken. Om die veldsterkte te bereken, word die konsep van die verhouding van potensiaal en veldsterkte gebruik:
Ex=−Δφ /Δx.
Onder sulke toestande word die rigting van die intensiteitsvektor longitudinaal relatief tot die dipool-as aangedui. Om sy modulus te bereken, is die standaardformule van toepassing.
Belangrikverduidelikings
Daar moet in ag geneem word dat die verswakking van die elektriese dipoolveld vinniger plaasvind as wat dit 'n puntlading ervaar. Die verval van die dipoolveldpotensiaal is omgekeerd eweredig aan die kwadraat van die afstand, en die veldsterkte is omgekeerd eweredig aan die kubus van die afstand.
Deur soortgelyke, maar meer omslagtige metodes te gebruik, word die parameters van die potensiaal en veldsterkte van die dipool by arbitrêre punte gevind, waarvan die posisieparameters bepaal word deur gebruik te maak van so 'n berekeningsmetode soos poolkoördinate: die afstand na die middelpunt van die elektriese dipool (r) en die hoek (θ).
Berekening met behulp van spanningsvektor
Die konsep van die intensiteitsvektor E word in twee punte verdeel:
- Radiaal (Er), wat in die lengterigting relatief tot die reguitlyn gerig is.
- So 'n reguit lyn verbind die gespesifiseerde punt en die middelpunt van die dipool met die loodlyn daarop Eθ.
Hierdie ontbinding van elke komponent is gerig op die verloop van verandering wat plaasvind met alle koördinate van die punt wat waargeneem moet word. Jy kan dit vind deur die verhouding wat veldsterkte-aanwysers met potensiële wysigings in verband bring.
Om die vektorkomponent by die veldsterkte te vind, is dit belangrik om die aard van die verband vas te stel in die potensiële veranderinge wat plaasvind as gevolg van die verplasing van die waarnemingspunt in die rigting van die vektore.
Bereken die loodregte komponent
Wanneer klaarVir hierdie prosedure is dit belangrik om in ag te neem dat die uitdrukking vir die grootte by 'n klein loodregte verplasing bepaal sal word deur die hoek te verander: Δl=rΔθ. Die grootte parameters vir hierdie veldkomponent sal gelyk wees.
Nadat die verhouding verkry is, is dit moontlik om die veld van die elektriese dipool by 'n arbitrêre punt te bepaal om 'n prentjie te bou met die kraglyne van hierdie veld.
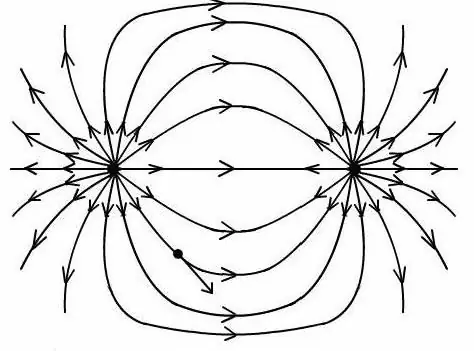
Dit is belangrik om in ag te neem dat alle formules vir die bepaling van die potensiaal en veldsterkte van 'n dipool slegs werk op die produk van die waardes wat een dipoollading het en die afstand tussen hulle.
Dipool-oomblik
Die titel van die beskryfde werk is 'n volledige beskrywing van die elektriese tipe eienskappe. Dit het die naam "dipoolmoment van die stelsel".
Deur definisie van 'n dipool, wat 'n stelsel van puntladings is, kan uitgevind word dat dit gekenmerk word deur die teenwoordigheid van aksiale simmetrie, wanneer die as 'n reguit lyn is wat deur verskeie ladings gaan.
Om die volle kenmerk van die dipool te stel, dui die oriëntasierigting aan wat die as het. Vir die eenvoud van berekeninge kan die dipoolmomentvektor gespesifiseer word. Die waarde van sy grootte is gelyk aan die grootte van die dipoolmoment, en die rigtingvektor verskil deur die toeval daarvan en die as van die dipool. Dus, p=qa as a die rigting is van die vektor wat die negatiewe en positiewe ladings van die dipool verbind.
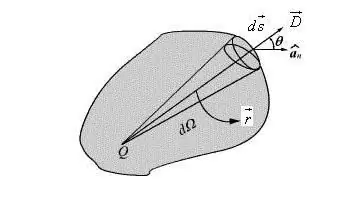
Die gebruik van so 'n eienskap van die dipool is gerieflik en maak dit in die meeste gevalle moontlik om die formule te vereenvoudig en die vorm daaraan te geevektor. Die beskrywing van die potensiaal van die dipoolveld by 'n punt van 'n arbitrêre rigting word in die vorm van 'n vektor geskryf.
Die bekendstelling van konsepte soos die vektorkenmerk van 'n dipool en sy dipoolmoment kan uitgevoer word deur gebruik te maak van 'n vereenvoudigde model − 'n puntlading in 'n eenvormige veld, wat 'n stelsel van ladings insluit, waarvan die geometriese afmetings hoef nie in ag geneem te word nie, maar dit is belangrik om die dipoolmoment te ken. Dit is 'n voorvereiste vir die uitvoer van berekeninge.
Hoe 'n dipool optree
Die gedrag van 'n dipool kan gesien word op die voorbeeld van so 'n situasie. Die posisie van twee puntladings het 'n vaste karakter van afstand relatief tot mekaar. Hulle is geplaas in die toestande van 'n dipool van 'n eenvormige elektriese veld. Het waarnemings oor die proses gemaak. In die lesse van fisika (elektrodinamika) word hierdie konsep in detail oorweeg. Van die veld na die lading word die werking van kragte uitgevoer:
F=±qE
Hulle is ewe groot en teenoorgestelde in rigting. Die aanwyser van die totale krag wat op die dipool inwerk is nul. Aangesien so 'n krag 'n effek op verskeie punte het, sal die totale moment wees:
M=Fa sin a=qEa sin a=pE sin a
met α die hoek wat die veldsterktevektore en die dipoolmomentvektore verbind. As gevolg van die teenwoordigheid van 'n kragmoment, neig die dipoolmoment van die sisteem om terug te keer na die rigtings van die elektriese veldsterktevektor.
Elektriese dipool is 'n konsep wat belangrik is om duidelik te verstaan. Jy kan meer daaroor op die internet lees. Dit kan ookom in graad 10 in fisikalesse by die skool te studeer, soos ons hierbo gepraat het.






