Die Titius-Bode-reël (soms bloot Bode se wet genoem) is die hipotese dat liggame in sommige wentelstelsels, insluitend die Son, langs halfasse roteer, afhangende van die planetêre volgorde. Die formule stel voor dat, na buite, elke planeet ongeveer twee keer so ver van die Son as die vorige een sal wees.
Die hipotese het die wentelbane van Ceres (in die asteroïdegordel) en Uranus korrek voorspel, maar kon nie die wentelbaan van Neptunus bepaal nie en is uiteindelik deur die sonnestelsel-vormingsteorie vervang. Dit is vernoem na Johann Daniel Titius en Johann Elert Bode.

Origins
Die eerste vermelding van 'n reeks wat Bode se wet benader, kan gevind word in David Gregory se Elements of Astronomy, wat in 1715 gepubliseer is. Daarin sê hy: “… aangeneem dat die afstand van die Son na die Aarde in tien gelyke dele verdeel word, waarvan die afstand van Mercurius ongeveer vier sal wees, vanaf Venus sewe, vanaf Mars vyftien, vanaf Jupiter twee-en-vyftig, en van Saturnus vyf en negentig'n Soortgelyke voorstel, waarskynlik deur Gregory geïnspireer, verskyn in 'n werk wat in 1724 deur Christian Wolff gepubliseer is.
In 1764 het Charles Bonnet in sy boek Contemplation of Nature gesê: "Ons ken die sewentien planete waaruit ons sonnestelsel bestaan [dit is die hoofplanete en hul satelliete], maar ons is nie seker dat hulle is nie meer nie." Hierby het Johann Daniel Titius in sy 1766-vertaling van Bonnet se werk twee eie paragrawe onderaan bladsy 7 en boaan bladsy 8 gevoeg. Die nuwe geïnterpoleerde paragraaf word nie in Bonnet se oorspronklike teks gevind nie: ook nie in die Italiaanse ook nie Engelse vertalings van die werk nie.
Ontdekking van Titius
Daar is twee dele in die geïnterkaleerde teks van Titius. Die eerste verduidelik die volgorde van planetêre afstande vanaf die Son. Dit bevat ook 'n paar woorde oor die afstand van die Son na Jupiter. Maar dit is nie die einde van die teks nie.
Dit is die moeite werd om 'n paar woorde te sê oor die formule van die Titius-Bode-reël. Gee aandag aan die afstande tussen die planete en vind uit dat byna almal van mekaar geskei is in 'n verhouding wat ooreenstem met hul liggaamsgroottes. Deel die afstand van die Son na Saturnus deur 100 dele; dan word Mercurius deur vier sulke dele van die Son geskei; Venus - in 4 + 3=7 sulke dele; Aarde - by 4+6=10; Mars - by 4+12=16.
Maar let op dat daar van Mars na Jupiter 'n afwyking van hierdie so presiese vordering is.’n Ruimte van 4+24=28 sulke dele volg vanaf Mars, maar tot dusver is nog nie’n enkele planeet daar ontdek nie. Maar moet die Here Argitek hierdie plek leeg laat? Nooit nie. Duskom ons neem aan dat hierdie ruimte sonder twyfel aan die nog onontdekte mane van Mars behoort, en voeg by dat Jupiter dalk nog 'n paar kleiner mane om hom het wat nog nie deur enige teleskoop gesien is nie.

Rise of the Bode
In 1772 voltooi Johann Elert Bode, op die ouderdom van vyf-en-twintig, die tweede uitgawe van sy astronomiese kompendium Anleitung zur Kenntniss des gestirnten Himmels ("Gids tot die kennis van die sterrehemel"), waarop hy het die volgende voetnoot bygevoeg, wat oorspronklik nie verkry is nie, maar in latere weergawes opgemerk is. In Bode se memoires kan 'n mens 'n verwysing na Titius vind met 'n duidelike erkenning van sy gesag.

Opinion Bode
Dit is hoe die Titius-Bode-reël in die aanbieding van laasgenoemde klink: as die afstand van die Son na Saturnus gelykstaande aan 100 geneem word, dan word Mercurius van die Son geskei deur vier sulke dele. Venus - 4+3=7. Aarde - 4+6=10. Mars - 4+12=16.
Nou is daar 'n gaping in hierdie geordende vordering. Na Mars volg 'n ruimte met 'n berekening van 4+24=28, waarin nog nie 'n enkele planeet gesien is nie. Kan ons glo dat die Stigter van die heelal hierdie ruimte leeg gelaat het? Natuurlik nie. Van hier af kom ons by die afstand van Jupiter in die vorm van berekening 4+48=52 en, uiteindelik, by die afstand van Saturnus - 4+96=100.

Hierdie twee stellings met betrekking tot alle spesifieke tipologie en orbitale radiusse kom blykbaar van ouds afsterrekunde. Baie van hierdie teorieë dateer terug na voor die sewentiende eeu.
Invloed
Titius was 'n student van die Duitse filosoof Christian Freiherr von Wolff (1679-1754). Die tweede deel van die ingevoegde teks in Bonnet se werk is gebaseer op von Wolff se 1723-werk, Vernünftige Gedanken von den Wirkungen der Natur.
Twintigste-eeuse literatuur ken die outeurskap van die Titius-Bode-reël aan 'n Duitse filosoof toe. Indien wel, kan Titius by hom leer. Nog 'n ouer verwysing is geskryf deur James Gregory in 1702 in sy Astronomiae Physicae et geometryae Elementa, waar die volgorde van planetêre afstande 4, 7, 10, 16, 52 en 100 'n meetkundige progressie van die verhouding 2 geword het.
Dit is Newton se naaste formule, en is ook gevind in die geskrifte van Benjamin Martin en Thomas Ceard jare voor Bonnet se boek in Duitsland gepubliseer is.
Verdere werk en praktiese implikasies
Titius en Bode het gehoop dat die wet tot die ontdekking van nuwe planete sou lei, en inderdaad, die ontdekking van Uranus en Ceres, waarvan die afstand goed met die wet ooreenstem, het bygedra tot die aanvaarding daarvan deur die wetenskaplike wêreld.
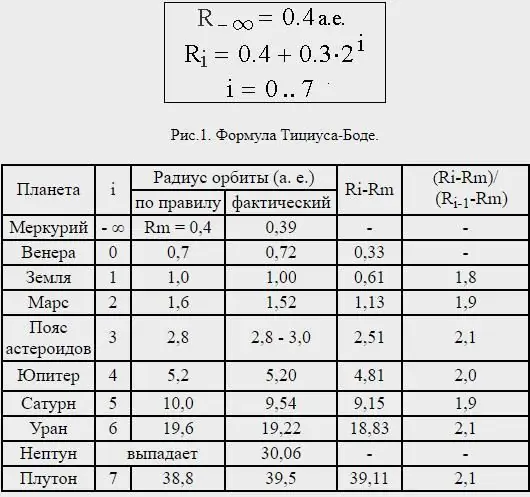
Neptunus se afstand was egter baie inkonsekwent, en in werklikheid is Pluto - wat nou nie as 'n planeet beskou word nie - op 'n gemiddelde afstand wat rofweg ooreenstem met die Titius-Bode-wet wat vir die volgende planeet buite Uranus voorspel is.
Die oorspronklik gepubliseerde wet is ongeveer bevredig deur alle bekende planete - Mercurius en Saturnus - met 'n gaping tussenvierde en vyfde planete. Dit is as 'n interessante, maar nie van groot belang nie, figuur beskou tot met die ontdekking van Uranus in 1781, wat in die reeks pas.
Op grond van hierdie ontdekking het Bode 'n soektog na 'n vyfde planeet gevra. Ceres, die grootste voorwerp in die asteroïdegordel, is in 1801 op Bode se voorspelde posisie gevind. Bode se wet is algemeen aanvaar totdat Neptunus in 1846 ontdek is en getoon is dat dit strydig met die wet was.
Terselfdertyd het 'n groot aantal asteroïdes wat in die gordel ontdek is, Ceres uit die lys van planete gekruis. Bode se wet is in 1898 deur die sterrekundige en logikus Charles Sanders Peirce bespreek as 'n voorbeeld van foutiewe redenasie.

Ontwikkeling van die probleem
Die ontdekking van Pluto in 1930 het die probleem verder gekompliseer. Alhoewel dit nie ooreenstem met die posisie wat deur Bode se wet voorspel is nie, het dit gegaan oor die posisie wat die wet vir Neptunus voorspel het. Die daaropvolgende ontdekking van die Kuiper-gordel, en veral die voorwerp Eris, wat meer massief as Pluto is, maar nie aan Bode se wet voldoen nie, het die formule egter verder gediskrediteer.
Serda se bydrae
Die Jesuïet Thomas Cerda het die beroemde sterrekundekursus in Barcelona in 1760 by die Koninklike Leerstoel vir Wiskunde aan die College of Sant Jaume de Cordelle (Imperial and Royal Seminary of the Nobles of Cordell) gegee. In Cerdas se Tratado verskyn planetêre afstande, verkry deur Kepler se derde wet toe te pas, met 'n akkuraatheid van 10-3.
As ons as 10 die afstand vanaf die Aarde enrond af na heelgetal, meetkundige progressie [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, van n=2 tot n=8, kan uitgedruk word. En met behulp van 'n sirkelvormige eenvormige fiktiewe beweging na die Kepler-anomalie, kan die Rn-waardes wat ooreenstem met die verhoudings van elke planeet verkry word as rn=(Rn - R1) / (Rn-1 - R1), wat lei tot 1,82; 1, 84; 1, 86; 1.88 en 1.90, waar rn=2 - 0.02 (12 - n) 'n eksplisiete verband is tussen die Kepleriaanse kontinuïteit en die Titius-Bode-wet, wat as 'n ewekansige numeriese toeval beskou word. Die resultaat van die berekening is naby aan twee, maar die twee kan wel beskou word as 'n afronding van die getal 1, 82.

Die planeet se gemiddelde spoed van n=1 tot n=8 verminder afstand vanaf die Son en verskil van die eenvormige afname by n=2 om te herstel van n=7 (orbitale resonansie). Dit beïnvloed die afstand van die Son na Jupiter. Die afstand tussen alle ander objekte binne die raamwerk van die berugte reël waaraan die artikel gewy word, word egter ook deur hierdie wiskundige dinamika bepaal.
Teoretiese aspek
Daar is geen soliede teoretiese verduideliking onderliggend aan die Titius-Bode-reël nie, maar dit is moontlik dat gegewe die kombinasie van orbitale resonansie en gebrek aan grade van vryheid, enige stabiele planetêre stelsel 'n hoë waarskynlikheid het om die model te herhaal wat beskryf word in hierdie teorie deur die twee wetenskaplikes.
Omdat dit dalk 'n wiskundige toeval is en nie 'n "natuurwet" nie, word dit soms 'n reël eerder as 'n "wet" genoem. Astrofisikus Alan Boss voer egter aan dat dit eenvoudig istoeval, en die planetêre wetenskapjoernaal Icarus aanvaar nie meer artikels wat probeer om verbeterde weergawes van die "wet" te verskaf nie.
Orbitale resonansie
Orbitale resonansie van groot wentelende liggame skep streke rondom die Son wat nie langtermyn-stabiele wentelbane het nie. Planeetvormingsimulasieresultate ondersteun die idee dat 'n ewekansig gekose stabiele planetêre stelsel waarskynlik aan die Titius-Bode-reël sal voldoen.

Dubrulle en Graner
Dubrulle en Graner het gewys dat kragwet afstandreëls 'n gevolg kan wees van modelle van ineenstortende wolke van planetêre stelsels wat twee simmetrieë het: rotasie-invariansie (die wolk en sy inhoud is aksimmetries) en skaal-invariansie (die wolk en sy inhoud lyk dieselfde op alle skale).
Laasgenoemde is 'n kenmerk van baie verskynsels wat vermoedelik 'n rol speel in planeetvorming, soos onstuimigheid. Die afstand van die Son na die planete van die sonnestelsel, voorgestel deur Titius en Bode, is nie in die raamwerk van die studies van Dubrulle en Graner hersien nie.






