Piramide saam met 'n prisma is 'n perfekte veelvlak in driedimensionele ruimte, hul meetkundige kenmerke word op hoërskool bestudeer. In hierdie artikel gaan ons kyk na wat piramides is, uit watter elemente dit bestaan, en ook kortliks die korrekte piramides karakteriseer.
Meetkundige figuurpiramide
Vanuit die oogpunt van meetkunde is die piramide 'n ruimtelike figuur wat uit een veelhoek en verskeie driehoeke bestaan. Om hierdie syfer te kry is redelik eenvoudig. Om dit te doen, neem 'n veelhoek met n sye, kies dan 'n arbitrêre punt in die ruimte wat nie in die vlak van die veelhoek sal lê nie, en verbind elke hoekpunt van die veelhoek met hierdie punt. Dit is duidelik dat die figuur wat op hierdie manier gevorm word, n driehoeke sal hê wat by een hoekpunt aan mekaar verbind is.
Om die geometriese vorm van die beskryfde figuur te visualiseer, kom ons neem 'n foto.

Dit wys 'n vierhoekige piramide waarvan die basis isvierhoek, en die syoppervlak word gevorm deur vier driehoeke wat 'n gemeenskaplike hoekpunt het.
Piramide-elemente
Soos enige veelvlak, word die piramide deur drie tipes elemente gevorm:
- rands;
- tops;
- ribs.
Gesigte is dele van vlakke wat die interne volume van 'n figuur van die omliggende ruimte skei. As die basis van die piramide 'n n-gon bevat, dan is die getal van sy vlakke altyd n+1. Hiervan is n sye driehoekig en een sy is die genoemde n-gonale basis.
Hokkepunte is punte waar drie of meer vlakke van 'n figuur sny. Die basisgebied bevat n hoekpunte, wat elk deur twee driehoekige vlakke en 'n basis gevorm word. Die punt waar n driehoekige sye bymekaarkom, word die bokant van die piramide genoem. Dus, die syfer onder oorweging bestaan uit n+1 hoekpunte.
Rande is reguit lyne wat verskyn wanneer twee vlakke mekaar sny. Elke rand word begrens deur twee hoekpunte aan sy punte. Enige piramide met 'n n-gon basis bevat 2n rande. Die helfte van hierdie getal, dit wil sê n, word uitsluitlik gevorm deur die snypunt van sydriehoeke.
Moontlike tipes syfers
Die naam van die figuur wat oorweeg word, word uniek bepaal deur die tipe veelhoek by die basis. Byvoorbeeld, as dit drie hoeke en drie kante het, dan sal die piramide driehoekig wees, indien vier - vierhoekig, ensovoorts.
Veelhoek kan konveks en konkaaf wees, sowel as gereelde en algemene tipe. Dit alles bepaal ook die voorkoms van die piramide.
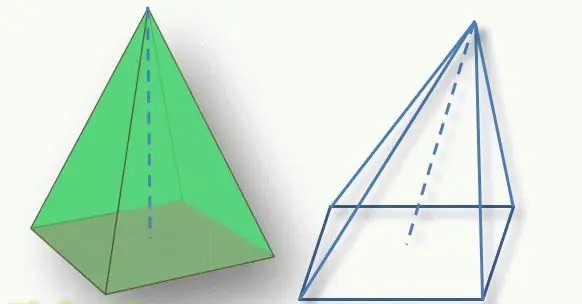
'n Belangrike punt in die bepaling van die tipe figuur is die posisie van die bokant van die piramide relatief tot sy basis. Die loodregte segment wat van bo na die veelhoekige basis getrek word, word die hoogte van die figuur genoem. As hierdie segment die basis by sy geometriese middelpunt sny (vir 'n driehoek is dit die snypunt van mediane, vir 'n vierhoek, die snypunt van diagonale), dan word die figuur 'n reguitlyn genoem. Andersins praat hulle van 'n skuins piramide.
As die n-hoek van die basis reëlmatig is (gelyksydige driehoek, vierkant, ens.), en die figuur is reguit, dan word dit 'n reëlmatige piramide genoem.
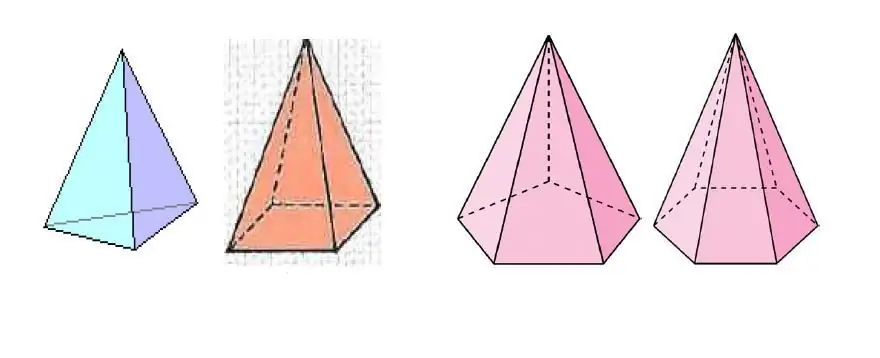
Die prent hierbo toon verskeie piramides, wat verskil in die aantal sye van die veelhoek by die basis.
Eienskappe van gereelde piramides
Hierdie piramides verskil van ander figure van hierdie klas deur 'n hoë mate van simmetrie. In hierdie verband is dit gerieflik om verskeie meetkundige berekeninge daarmee uit te voer, byvoorbeeld volume of oppervlakte.
'n Gereelde piramide bevat 'n n-gon aan sy basis, waarvan die oppervlakte uniek bepaal word uit die kennis van die lengte van sy sy. Die syoppervlak van die figuur word gevorm deur n identiese driehoeke, wat gelyksydig is. Die rande van 'n gereelde piramide wat op die laterale oppervlak geleë is, is gelyk aan mekaar. Die waarde van die lengte van hierdie rand word dikwels gebruik wanneer die apotem van 'n figuur bereken word en die oppervlakte bepaal word.
Die hoogte van 'n gereelde piramide is die tweede belangrike eienskap van die figuur (die eerste is die lengte van die randgronde). Hoogte word gebruik wanneer volume bereken word.
Enige vlak parallel aan die basis, wat die syvlakke van die piramide sny, lei tot die vorming van 'n veelhoekige snit. Dit is homoteties met betrekking tot die basisveelhoek. Die beskryfde snybewerking lei tot die vorming van 'n hele klas nuwe figure - afgekapte gereelde piramides.
Die bekendste piramides

Natuurlik is dit die gereelde vierhoekige piramides van die Egiptiese farao's. In 'n plek genaamd Giza, is daar meer as 100 van hierdie klipmonumente, waarvan die perfeksie van ontwerp en die akkuraatheid van die geometriese parameters wetenskaplikes tot vandag toe steeds verbaas. Die grootste daarvan is die Piramide van Cheops, wat sowat 146 meter hoog en sowat 230 meter lank is.
Waarvoor presies hierdie piramides gedien het, asook deur watter meganismes en wanneer hulle gebou is, weet niemand tot vandag toe nie.






