Proposisionele algebra is 'n presiese wetenskap wat nie kompromieë aangaan nie. Om voorbeelde met voegwoord, disjunksie, implikasie, ensovoorts op te los, kan jy 'n waarheidstabel in die Excel-toepassing bou. Dit is toegerus met 'n stel logiese funksies wat die proses om die resultaat te vind outomatiseer en vergemaklik.
Wiskundige logika: basiese konsepte
Aristoteles word beskou as die stigter van formele logika. In die 17de eeu G. Leibniz het voorgestel om simbole in te voer om stellings te definieer. D. Buhl het die verworwe kennis gekonsolideer en vir die eerste keer sinne met simbole gemerk.
Skematies word "WAAR" vervang met 1, en "ONWAAR" met 0.
Onder die verklaring word enige verklarende sin verstaan wat enige inligting gee en in staat is om die waarde van waarheid of valsheid te aanvaar. In algebra word logika uit die semantiese lading van sinne geabstraheer en neem slegs logiese waardes in ag.
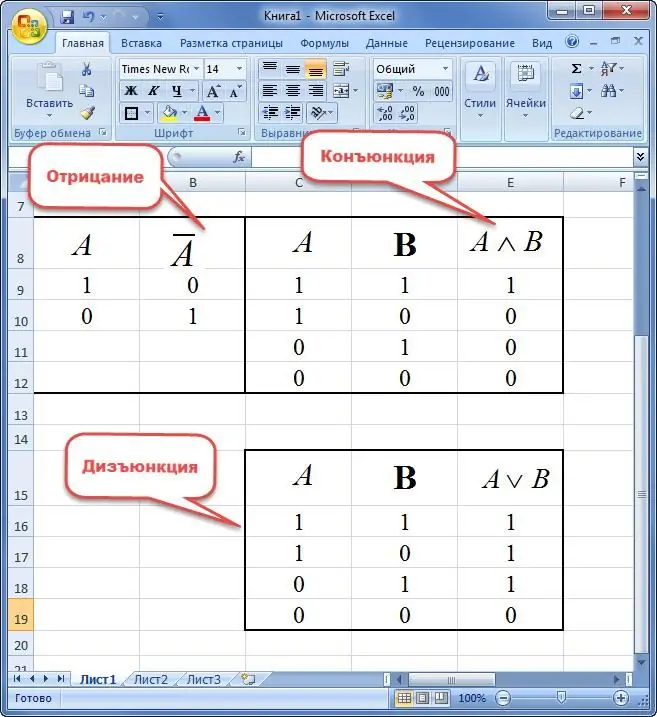
Negasie is 'n nuwe uitdrukking wat die waarde van waar neem as dit onwaar is en omgekeerd.
Verbinding van tweeveranderlikes word 'n nuwe sin genoem, wat die waarde van waarheid neem in die geval van gelyktydige aanduiding "1" en valsheid in ander situasies.
Die disjunksie van twee stellings word verstaan as 'n nuwe uitdrukking wat slegs die waarde "ONWAAR" neem as daar gelyktydig "0" en "WAAR" in ander variasies is.
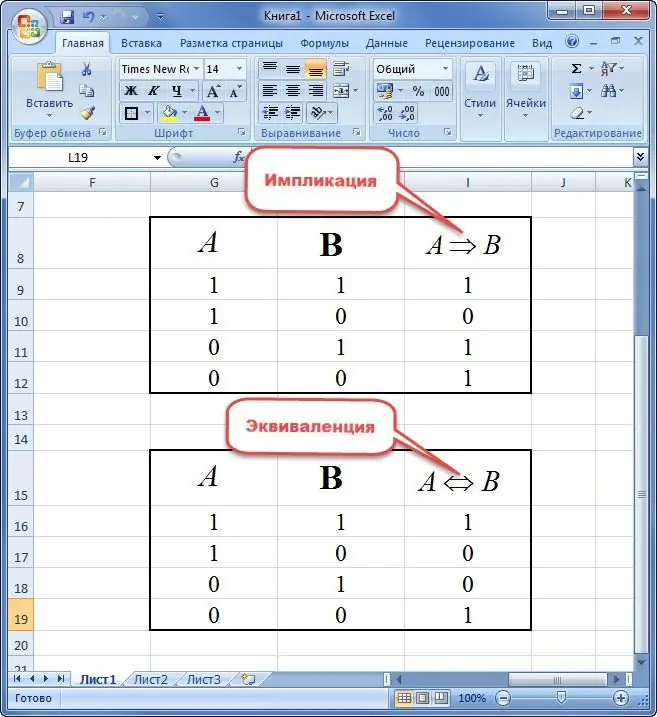
'n Implikasie van twee veranderlikes is 'n nuwe sin waarin:
- as die uitgangspunt waar is en die gevolg is onwaar, dan is die uitdrukking gelyk aan "0";
- stelling is gelyk aan "1" in ander gevalle.
Ekwivalent van twee veranderlikes word verstaan as 'n nuwe stelling wat slegs die waarde van waarheid aanvaar as die elemente dieselfde is. Andersins is die aanbod "0".
Logiese waardes van uitdrukkings word gewoonlik in tabelvorm aangebied. Daar is 'n ander naam vir hierdie soort inligting. Hulle sê dat jy vir 'n stelling 'n waarheidstabel moet bou. Dit spesifiseer die beginwaardes vir alle veranderlikes, en dan word die resultaat van die hele uitdrukking bereken.
Algorithme vir die implementering van berekeninge in logiese bewerkings
Om 'n waarheidstabel te bou, moet jy weet in watter volgorde die aksies uitgevoer word. In 'n uitdrukking met veelvuldige operandes word die berekening in die volgende volgorde uitgevoer:
- inversie (ontkenning);
- konjunksie (logiese funksie in Excel "AND");
- disjunction (booleaanse operateur in Excel "OF");
- implikasie (gevolg);
- ekwivalensie.
Daar is nog twee bewerkings, maar hul prioriteit is nie gedefinieer nie:
- Schaeffer se beroerte;
- Pierce-pyl.
Die berekeningsalgoritme verander as die uitdrukking tussen hakies ingesluit is.
Die volgorde van die bou van 'n tabelvorm vir logiese operandes in Excel
Voordat jy die waarde van 'n uitdrukking vind, moet jy die konsep van 'n logiese algebra-formule bestudeer. Die definisie sê dat dit 'n komplekse uitdrukking is, wat bestaan uit die eenvoudigste stellings wat deur logiese operande verbind word.
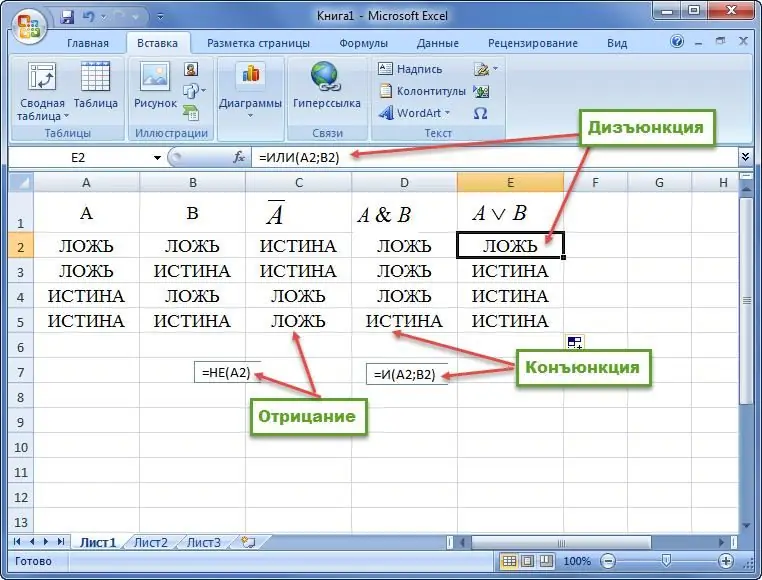
Voorbeeld 1. Konstrueer 'n waarheidstabel vir voegwoord, disjunksie en ontkenning.
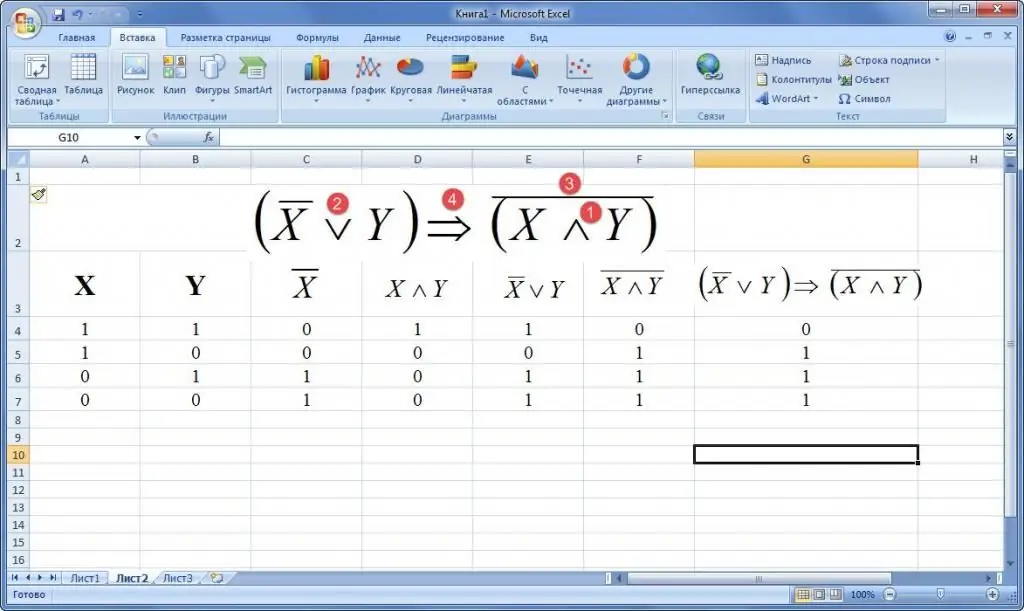
Voorbeeld 2. Gegee 'n formule vir die algebra van logika. Bou 'n waarheidstabel. Voorbeelde word hieronder gegee.
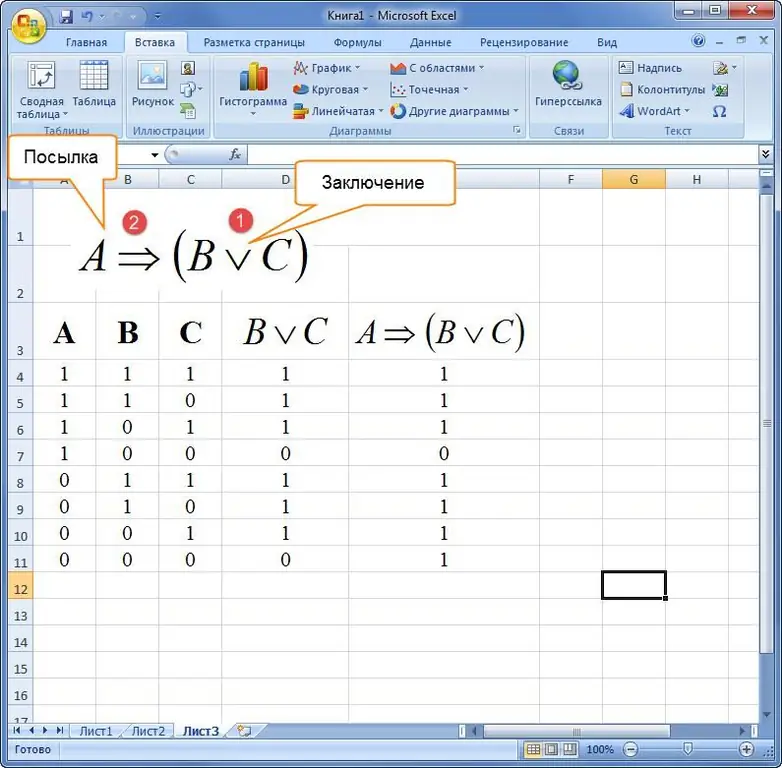
Voorbeeld 3. Hoe om 'n waarheidstabel in Excel te bou, gegee 'n formule van logiese algebra in 'n verbale beskrywing. Sê: "As 'n driehoek gelyksydig is, dan is al sy rande gelyk of al sy hoeke is gelyk."
Eers moet jy die saamgestelde sin in minimale elemente ontleed:
- Die eerste deel van die uitdrukking: A="gelyksydige driehoek".
- Tweede: B="alle kante van die figuur is gelyk".
- Derde: C="alle hoeke van 'n driehoek is gelyk".
Daarna word 'n uitdrukking saamgestel en opgelos in die Excel-sagtewarepakket.
Wanneer jy waarheidstabelle saamstel, is dit belangrik om die volgorde van bewerkings te onthou.






