Soos jy weet, behoort enige fisiese hoeveelheid aan een van twee tipes, dit is óf skalêr óf vektor. In hierdie artikel sal ons sulke kinematiese eienskappe soos spoed en versnelling oorweeg, en ook wys waarheen die versnelling en spoedvektore gerig is.
Wat is spoed en versnelling?
Albei die hoeveelhede wat in hierdie paragraaf genoem word, is belangrike kenmerke van enige soort beweging, of dit nou 'n liggaam in 'n reguit lyn of langs 'n geboë pad beweeg.
Speed is die tempo waarteen koördinate oor tyd verander. Wiskundig is hierdie waarde gelyk aan die tydafgeleide van die afstand afgelê, dit wil sê:
v¯=dl¯/dt.
Hier word die vektor l¯ vanaf die beginpunt van die pad na die eindpunt gerig.
Op sy beurt is versnelling die spoed waarmee die spoed self in tyd verander. In die vorm van 'n formule kan dit so geskryf word:
a¯=dv¯/dt.
Natuurlik, neem die tweede afgeleide vanverplasingsvektor l¯ mettertyd, sal ons ook die waarde van die versnelling kry.
Aangesien spoed in meter per sekonde gemeet word, word versnelling, volgens die geskrewe uitdrukking, in meter per sekonde kwadraat gemeet.

Waar is die versnelling- en snelheidsvektore?
In fisika word enige meganiese beweging van 'n liggaam gewoonlik gekenmerk deur 'n sekere trajek. Laasgenoemde is een of ander denkbeeldige kromme waarlangs die liggaam in die ruimte beweeg. Byvoorbeeld, 'n reguit lyn of 'n sirkel is uitstekende voorbeelde van algemene bewegingspaaie.
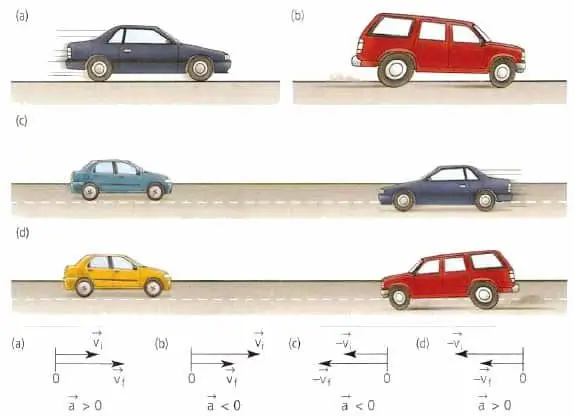
Die liggaam se snelheidsvektor is altyd in die rigting van beweging gerig, ongeag of die liggaam stadiger of versnel, of dit in 'n reguit lyn of langs 'n kromme beweeg. Gesproke in meetkundige terme, is die snelheidsvektor tangensiaal gerig na die punt van die trajek waarin die liggaam tans geleë is.
Die versnellingsvektor van 'n materiaal- of liggaamspunt het niks met spoed te doen nie. Hierdie vektor is gerig in die rigting van spoedverandering. Byvoorbeeld, vir reglynige beweging kan die waarde a¯ óf saamval in rigting met v¯ óf teenoorgestelde van v¯ wees.
Dwing wat op die liggaam inwerk en versnelling
Ons het uitgevind dat die versnellingsvektor van die liggaam gerig is op die verandering van die snelheidsvektor. Dit is egter nie altyd maklik om te bepaal hoe die spoed op 'n gegewe punt in die trajek verander nie. Verder, om die verandering in spoed te bepaal, is dit nodig om die operasie uit te voervektor verskille. Om hierdie probleme met die bepaling van die rigting van die vektor a¯ te vermy, is daar 'n ander manier om vinnig uit te vind.
Hieronder is Newton se bekende en bekende wet aan elke student:
F¯=ma¯.
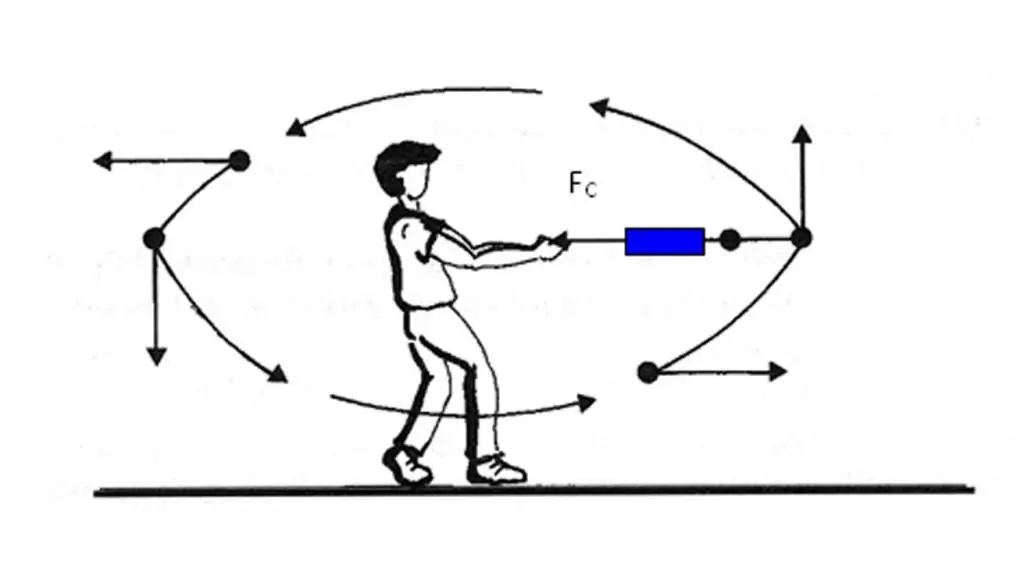
Die formule wys dat die oorsaak van versnelling in liggame die krag is wat op hulle inwerk. Aangesien die massa m 'n skalaar is, is die kragvektor F¯ en die versnellingsvektor a¯ in dieselfde rigting. Hierdie feit moet onthou word en in die praktyk toegepas word wanneer dit ook al nodig is om die rigting van die hoeveelheid a¯ te bepaal.
As verskeie verskillende kragte op die liggaam inwerk, dan sal die rigting van die versnellingsvektor gelyk wees aan die resulterende vektor van alle kragte.
Sirkulêre beweging en versnelling
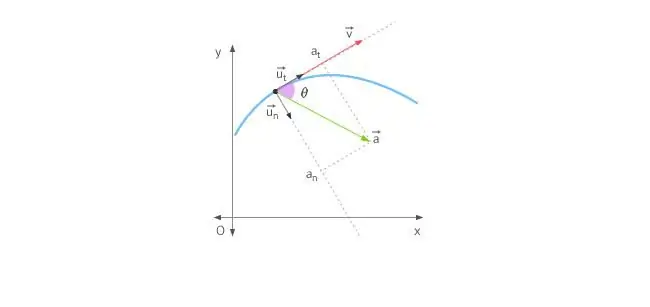
Wanneer 'n liggaam in 'n reguit lyn beweeg, word die versnelling óf vorentoe óf agtertoe gerig. In die geval van beweging in 'n sirkel, word die situasie gekompliseer deur die feit dat die snelheidsvektor voortdurend sy rigting verander. In die lig van bogenoemde word die totale versnelling deur sy twee komponente bepaal: tangensiële en normale versnellings.
Tansiële versnelling is presies dieselfde as die snelheidsvektor gerig, of daarteen. Met ander woorde, hierdie versnellingskomponent is langs die raaklyn aan die trajek gerig. Tangensiële versnelling beskryf die verandering in die modulus van die spoed self.
Normale versnelling word langs die normaal na die gegewe punt van die trajek gerig, met inagneming van die kromming daarvan. In die geval van sirkelbeweging dui die vektor van hierdie komponent aanna die middelpunt, dit wil sê, die normale versnelling word langs die rotasieradius gerig. Hierdie komponent word dikwels sentripetaal genoem.
Volversnelling is die som van hierdie komponente, so sy vektor kan arbitrêr gerig word met betrekking tot die sirkellyn.
As die liggaam roteer sonder om die lineêre snelheid te verander, dan is daar slegs 'n nie-nul normale komponent, dus is die volle versnellingsvektor na die middel van die sirkel gerig. Let daarop dat hierdie sentrum ook beïnvloed word deur 'n krag wat die liggaam op sy baan hou. Byvoorbeeld, die gravitasiekrag van die Son hou ons Aarde en ander planete in hul wentelbane.






