'n Lineêre funksie is 'n reguit lyn wat langs 'n oppervlak getrek word. Dit kan in verskillende tipes en modelle verdeel word. Hieronder sal ons die formules oorweeg om dit te verkry, sowel as om die volmaaktheid daarvan in die vliegtuig te bereik. In die tekeninge kan jy dit volledig verifieer en verstaan hoe dit moet lyk.
Lineêre funksie y=kx + b
Hierdie waarde is 'n akkurate maatstaf van 'n veranderlike in een aansig. Inkrement verwys na die basiese eienskap van 'n lineêre funksie, dit word eweredig aan die verhoogde argument. Met ander woorde, die funksie verteenwoordig 'n veralgemening van direkte proporsionaliteit. 'n Reguitlyn is 'n grafiek van 'n lineêre funksie. Dit is waar sy naam vandaan kom. Een reële veranderlike raak 'n ander reële funksie.
Properties
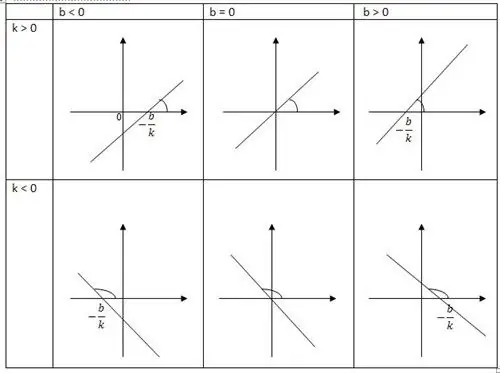
Lineêre funksie is 'n generatriks van 'n reguit lyn, wat 'n positiewe rigting van die x-as het. Een van sy bepalende hellingsfaktore is k, dit bepaal die raaklyn van die hoek a. Die reguitlyn wat in die positiewe rigting van die x-as gevorm word, is k. Die ander koördinaat b dui aanpuntkoördinate, sowel as die snypunt van die lyn met die as.
Wat is nie-lineêre funksies?
Funksies wat nie lineêr is nie, word nie-lineêr genoem. Dit is 'n wiskundige verband tussen veranderlikes. Nie-lineêre enes kan nie uitgedruk word as y=ax + b nie. Hierdie term word gebruik in daardie oomblikke wanneer dit nodig is om die algemene geval te bestudeer. Hierdie proses begin met die laer grade. In hierdie geval word kwadratiese regstellings oorweeg. So 'n funksie het deurlopende kromming.
Die beskoude nie-lineêre vergelyking is arbitrêr. 'n Voorbeeld van 'n nie-lineêre funksie is y=x2. Die terme "lineêre funksie" word dikwels gebruik, met 'n verfyning en die toevoeging van "homogeen". Dit kan toegepas word op 'n presiese lineêre kartering van X, wat 'n vektorruimte is. 'n Lineêre funksie is die hele stelsel soos dit.






