Wanneer hulle in fisika die meganiese beweging van liggame in die ruimte bestudeer, neem hulle altyd die gevolglike versnelling in ag. Kom ons kyk in die artikel wat versnelling is, en hoe dit in fisika aangedui word, en los ook 'n eenvoudige probleem op om hierdie waarde te bereken.
Wat is versnelling en wat is die tipes daarvan?
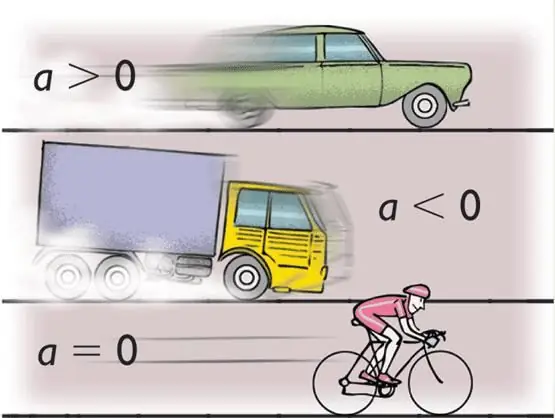
Verstaan die waarde onder die versnelling, waarvan die betekenis die spoed van verandering in die spoed van die liggaam is. Wiskundig word hierdie definisie soos volg geskryf:
a=dv/dt.
As die tydfunksie van spoed bekend is, dan is dit genoeg om sy eerste afgeleide te vind om die versnelling op 'n gegewe tydstip te bereken.
In fisika is die letter van versnelling die kleinletter Latyn a. Dit is egter die sogenaamde lineêre versnelling, wat gemeet word in eenhede van m/s2. Benewens dit is daar ook hoekversnelling. Dit toon die verandering in hoeksnelheid en word uitgedruk in eenhede van rad/s2. Hierdie tipe versnelling word aangedui deur die Griekse kleinletter α (alfa). Somsdie letter ε (epsilon) word gebruik om dit aan te dui.
As die liggaam langs 'n geboë trajek beweeg, dan word die totale versnelling in twee komponente ontbind: tangensiaal (bepaal die verandering in spoed in grootte) en normaal (bepaal die verandering in spoed in rigting). Hierdie tipe versnelling word ook met die letters a aangedui, maar met die ooreenstemmende indekse: at en a. Normaal word dikwels sentripetaal genoem, en tangensiaal word dikwels tangens genoem.
Laastens is daar nog 'n soort versnelling wat plaasvind wanneer liggame vrylik in die planeet se gravitasieveld val. Dit word aangedui met die letter g.
Probleem in fisika vir versnelling
Dit is bekend dat die liggaam in 'n reguit lyn beweeg. Sy spoed oor tyd word bepaal deur die volgende wet:
v=2t2-t+4.
Dit is nodig om die versnelling te bereken wat die liggaam op tyd t=2.5 sekondes sal hê.
Volg die definisie van a, kry ons:
a=dv/dt=4t - 1.
Dit wil sê, die waarde a hang lineêr van tyd af. Dit is eienaardig om daarop te let dat die versnelling op die aanvanklike oomblik (t=0) negatief was, dit wil sê gerig teen die snelheidsvektor. Ons kry die antwoord op die probleem deur t=2.5 sekondes in hierdie vergelyking te vervang: a=9 m/s2.






