Tipiese beligtingseffekte wat elke persoon dikwels in die alledaagse lewe teëkom, is refleksie en breking. In hierdie artikel sal ons die geval oorweeg wanneer beide effekte hulself binne dieselfde proses manifesteer, ons sal praat oor die verskynsel van interne totale refleksie.
Ligweerkaatsing
Voordat jy die verskynsel van interne totale weerkaatsing van lig oorweeg, moet jy kennis maak met die uitwerking van gewone refleksie en breking. Kom ons begin met die eerste een. Vir eenvoud sal ons slegs lig oorweeg, hoewel hierdie verskynsels kenmerkend is van 'n golf van enige aard.
Refleksie word verstaan as 'n verandering van een reglynige trajek, waarlangs 'n ligstraal beweeg, na 'n ander reglynige baan, wanneer dit 'n hindernis op sy pad teëkom. Hierdie effek kan waargeneem word wanneer 'n laserwyser na 'n spieël gerig word. Die voorkoms van beelde van die lug en bome wanneer na die wateroppervlak gekyk word, is ook die gevolg van die weerkaatsing van sonlig.

Die volgende wet is geldig vir refleksie: hoekeinval en refleksie lê in dieselfde vlak saam met die loodreg op die reflekterende oppervlak en is gelyk aan mekaar.
Refraksie van lig
Die effek van breking is soortgelyk aan refleksie, net dit vind plaas as die hindernis in die pad van die ligstraal nog 'n deursigtige medium is. In hierdie geval word 'n deel van die aanvanklike straal vanaf die oppervlak gereflekteer, en 'n deel gaan na die tweede medium. Hierdie laaste deel word die gebreekte bundel genoem, en die hoek wat dit maak met die loodreg op die raakvlak word die brekingshoek genoem. Die gebreekte bundel lê in dieselfde vlak as die gereflekteerde en invallende bundel.
Sterk voorbeelde van breking is die breek van 'n potlood in 'n glas water of die bedrieglike diepte van 'n meer wanneer 'n persoon op sy bodem afkyk.

Wiskundig word hierdie verskynsel beskryf met behulp van Snell se wet. Die ooreenstemmende formule lyk soos volg:
1 sin (θ1)=n2 sin (θ) 2).
Hier word die invals- en brekingshoeke onderskeidelik as θ1 en θ2 aangedui. Die hoeveelhede n1, n2 weerspieël die spoed van lig in elke medium. Hulle word die brekingsindekse van die media genoem. Hoe groter n, hoe stadiger beweeg die lig in 'n gegewe materiaal. Byvoorbeeld, in water is die spoed van lig 25% minder as in lug, so daarvoor is die brekingsindeks 1,33 (vir lug is dit 1).
Die verskynsel van totale interne refleksie
Die wet van breking van lig lei tot een'n interessante resultaat wanneer die straal voortplant vanaf 'n medium met groot n. Kom ons kyk in meer besonderhede na wat in hierdie geval met die balk sal gebeur. Kom ons skryf Snell se formule uit:
1 sin (θ1)=n2 sin (θ) 2).
Ons sal aanneem dat n1>n2. In hierdie geval, vir die gelykheid om waar te bly, moet θ1 minder as θ2 wees. Hierdie gevolgtrekking is altyd geldig, aangesien slegs hoeke van 0o tot 90o in ag geneem word, waarbinne die sinusfunksie voortdurend toeneem. Dus, wanneer 'n digter optiese medium vir 'n minder digte medium verlaat word (n1>n2), wyk die straal meer van die normale af.
Kom ons vergroot nou die hoek θ1. Gevolglik sal die oomblik kom wanneer θ2 gelyk sal wees aan 90o. 'n Wonderlike verskynsel vind plaas: 'n straal wat deur 'n digter medium uitgestraal word, sal daarin bly, dit wil sê, daarvoor sal die koppelvlak tussen twee deursigtige materiale ondeursigtig word.
Kritiese hoek
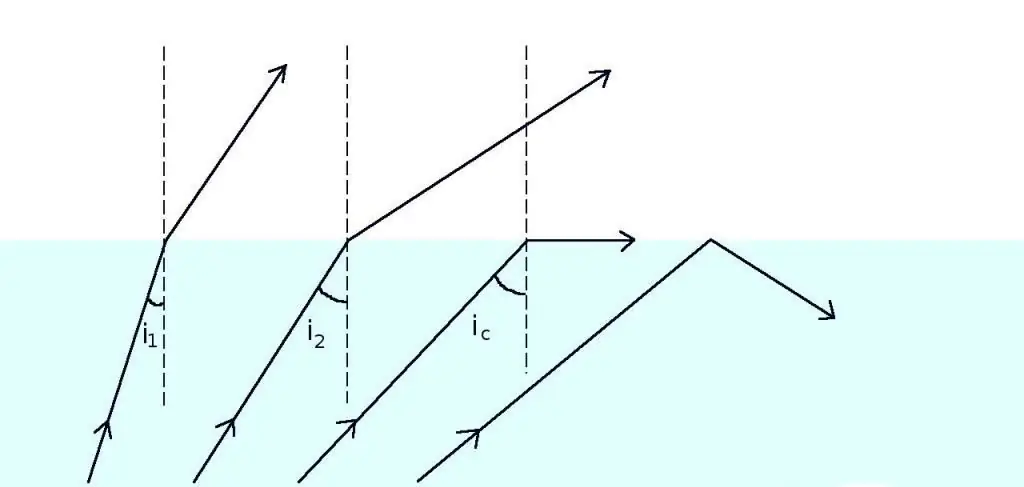
Die hoek θ1, waarvoor θ2=90o, genoem word krities vir die oorwoë paar media. Enige straal wat die koppelvlak tref teen 'n hoek groter as die kritieke hoek, word heeltemal in die eerste medium gereflekteer. Vir die kritiese hoek θc kan 'n mens 'n uitdrukking skryf wat direk uit Snell se formule volg:
sin (θc)=n2 / n1.
Ifdie tweede medium is lug, dan word hierdie gelykheid vereenvoudig tot die vorm:
sin (θc)=1 / n1.
Byvoorbeeld, die kritieke hoek vir water is:
θc=arcsin (1/1, 33)=48, 75o.
As jy na die bodem van die swembad duik en opkyk, kan jy die lug en wolke net bo jou eie kop daaroor sien hardloop, op die res van die wateroppervlak sal net die mure van die swembad sigbaar wees.
Uit bogenoemde redenasie is dit duidelik dat, anders as breking, totale refleksie nie 'n omkeerbare verskynsel is nie, dit kom slegs voor wanneer van 'n digter na 'n minder digte medium beweeg word, maar nie andersom nie.
Totale refleksie in die natuur en tegnologie
Miskien is die mees algemene effek in die natuur, wat onmoontlik is sonder totale refleksie, die reënboog. Die kleure van die reënboog is die gevolg van die verspreiding van wit lig in reëndruppels. Wanneer die strale egter binne-in hierdie druppels beweeg, ervaar hulle óf enkel óf dubbel interne refleksie. Daarom verskyn die reënboog altyd dubbel.
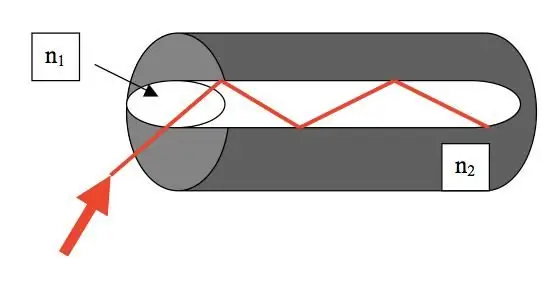
Die verskynsel van interne totale refleksie word in optieseveseltegnologie gebruik. Danksy optiese vesels is dit moontlik om elektromagnetiese golwe sonder verlies oor lang afstande uit te stuur.






