Wanneer ewekniebeoordeling byvoorbeeld die mededingendheid van produkte beoordeel, is dit nodig, soos in enige wetenskaplike werk, om statistiese dataverwerking uit te voer. Laasgenoemde begin met die bepaling van die konsekwentheid van deskundige menings, waarvan die numeriese uitdrukking die konkordansiekoëffisiënt is.
Hoekom het ons 'n kundige konsensusbeoordeling nodig?
Hierdie assessering is eerstens nodig, want die menings van kundiges kan grootliks verskil oor die geskatte parameters. Aanvanklik word die assessering uitgevoer deur die aanwysers te rangskik en 'n sekere koëffisiënt van betekenis (gewig) aan hulle toe te ken. 'n Inkonsekwente rangorde lei daartoe dat hierdie koëffisiënte statisties onbetroubaar is. Die menings van kundiges met hul vereiste getal (meer as 7-10) moet volgens die normale wet versprei word.
Die konsep van die konkordansiekoëffisiënt
So. Konsekwentheid is konkordansie. Die koëffisiënt is 'n dimensielose hoeveelheid wat die verhouding van die dispersie tot die maksimum verspreiding in die algemene geval toon. Kom ons veralgemeen hierdie konsepte.
Konkordansiekoëffisiënt is 'n getal van 0 tot 1, wat die konsekwentheid van deskundige menings toon wanneersommige eiendomme te rangskik. Hoe nader hierdie waarde aan 0 is, hoe laer word die konsekwentheid beskou. As die waarde van hierdie koëffisiënt minder as 0,3 is, word die menings van kundiges as inkonsekwent beskou. Wanneer die waarde van die koëffisiënt in die reeks van 0,3 tot 0,7 is, word die konsekwentheid as gemiddeld beskou. 'n Waarde groter as 0,7 word as hoë konsekwentheid beskou.
Gebruiksake
Wanneer statistiese navorsing gedoen word, kan situasies ontstaan waarin 'n voorwerp nie deur twee rye gekenmerk kan word nie, wat statisties verwerk word deur die konkordansiekoëffisiënt te gebruik, maar deur verskeie reekse, wat dienooreenkomstig deur kundiges met dieselfde vlak van professionaliteit in 'n sekere area.
Die konsekwentheid van die rangorde wat deur kundiges uitgevoer word, moet bepaal word om die korrektheid van die hipotese te bevestig dat kundiges relatief akkurate metings maak, wat die vorming van verskeie groeperings in kundige groepe moontlik maak, wat grootliks deur menslike faktore bepaal word, hoofsaaklik soos verskille in sienings, konsepte, verskillende wetenskaplike skole, die aard van professionele aktiwiteit, ens.
Kort beskrywing van die rangmetode. Die voordele en nadele daarvan
Wanneer die rangorde geplaas word, word die rangmetode gebruik. Die essensie daarvan lê in die feit dat elke eienskap van die voorwerp sy eie spesifieke rang toegeken word. Verder, elke deskundige wat in die deskundige groep ingesluit is, word hierdie rang toegekenonafhanklik, wat lei tot die behoefte om hierdie data te verwerk om die konsekwentheid van deskundige menings te identifiseer. Hierdie proses word uitgevoer deur die konkordansiekoëffisiënt te bereken.
Die hoofvoordeel van die rang-metode is die maklike implementering daarvan.
Die belangrikste nadele van die metode is:
- 'n klein aantal rangorde-voorwerpe, want wanneer hul getal 15-20 oorskry, word dit moeilik om objektiewe rangordetellings toe te ken;
- Op grond van die gebruik van hierdie metode bly die vraag hoe ver die bestudeerde voorwerpe van mekaar af is, oop.
Wanneer hierdie metode gebruik word, moet daar in ag geneem word dat die graderings op een of ander waarskynlikheidsmodel gebaseer is, dus moet dit met omsigtigheid toegepas word, gegewe die omvang.
Kendall se konkordansie-rangkoëffisiënt
Word gebruik om die verwantskap tussen kwantitatiewe en kwalitatiewe kenmerke wat homogene voorwerpe kenmerk, te bepaal en volgens dieselfde beginsel gerangskik.
Hierdie koëffisiënt word bepaal deur die formule:
t=2S/(n(n-1)), waar
S - die som van die verskille tussen die aantal rye en die aantal inversies op die tweede kenmerk;
n - aantal waarnemings.

Berekeningsalgoritme:
- Die x-waardes word in stygende of dalende volgorde gerangskik.
- Die y-waardes is gerangskik in die volgorde waarin hulle ooreenstem met die x-waardes.
- Vir elke opeenvolgende rang van y, bepaal hoeveel hoër rangwaardes daarop volg. Hulle word opgetel en die maatstaf van ooreenstemming van rye van range in x en y word bereken.
- Net so word die aantal range van y met laer waardes bereken, wat ook optel.
- Voeg die aantal range met hoër waardes by en die aantal range met laer waardes, wat lei tot die waarde S.
Hierdie koëffisiënt toon die verband tussen twee veranderlikes, en word in die meeste gevalle die Kendall-rangkorrelasiekoëffisiënt genoem. Sulke afhanklikheid kan grafies voorgestel word.
Bepaling van koëffisiënt
Hoe word dit gedoen? As die aantal gerangorde kenmerke of faktore 2 oorskry, word die konkordansiekoëffisiënt gebruik, wat in wese 'n veelvuldige variant van rangkorrelasie is.
Wees versigtig. Die berekening van die konkordansiekoëffisiënt is gebaseer op die verhouding van die afwyking van die som van kwadrate van range van die gemiddelde som van kwadrate van range, vermenigvuldig met 12, tot die kwadraat van deskundiges, vermenigvuldig met die verskil tussen die derdemag van die getal van voorwerpe en die aantal voorwerpe.
Berekeningsalgoritme
Om te verstaan waar die getal 12 vandaan kom in die teller van die berekeningsformule, kom ons kyk na die bepalingsalgoritme.
Vir elke reël met die geledere van 'n sekere deskundige, word die som van die range bereken, wat 'n ewekansige waarde is.
Die konkordansiekoëffisiënt word oor die algemeen gedefinieer as die verhouding van die variansieskatting (D) tot die maksimum waarde van die variansieskatting(Dmax). Kom ons formuleer agtereenvolgens die definisies van hierdie hoeveelhede.
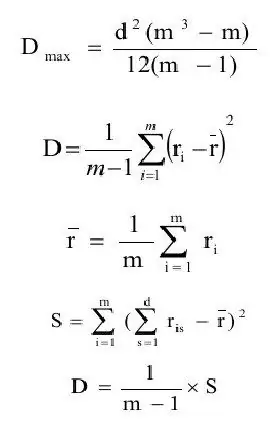
waar ravg - verwagting skatting;
m - aantal voorwerpe.
Deur die resulterende formules met betrekking tot D te vervang met Dmax kry ons die finale formule vir die konkordansiekoëffisiënt:
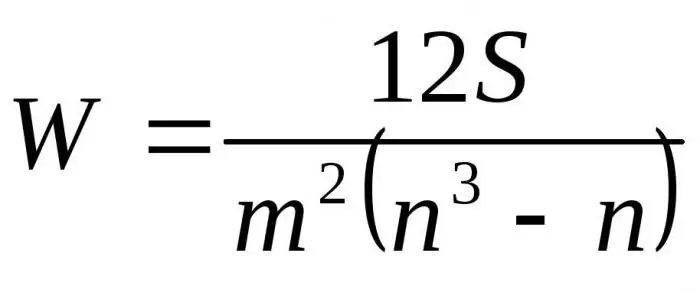
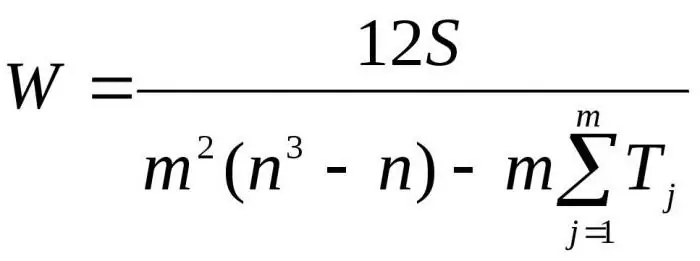
Hier is m die aantal kundiges, n is die aantal voorwerpe.
Die eerste formule word gebruik om die konkordansiefaktor te bepaal as daar geen verwante range is nie. Die tweede formule word gebruik as daar verwante geledere is.
Dus, die berekening van die konkordansiekoëffisiënt is verby. Wat is volgende? Die verkryde waarde word geëvalueer vir betekenisvolheid deur die Pearson-koëffisiënt te gebruik deur hierdie koëffisiënt te vermenigvuldig met die aantal kundiges en met die aantal vryheidsgrade (m-1). Die gevolglike maatstaf word met die tabelwaarde vergelyk, en as die waarde van die eerste die laaste oorskry, praat hulle van die betekenis van die koëffisiënt wat bestudeer word.
In die geval van verwante geledere, word die berekening van die Pearson-kriterium ietwat meer ingewikkeld en word uitgevoer deur die volgende verhouding: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Voorbeeld
Veronderstel dat die kundige metode die mededingendheid van botter wat in 'n kleinhandelnetwerk verkoop word, evalueer. Kom ons gee 'n voorbeeld van die berekening van die konkordansiekoëffisiënt. Voordat mededingendheid beoordeel word, is dit nodig om verbruiker te rangskikeienskappe van hierdie produk wat by die evaluering betrokke is. Kom ons neem aan dat hierdie eienskappe die volgende sal wees: smaak en reuk, konsekwentheid en voorkoms, kleur, verpakking en etikettering, vetinhoud, handelsnaam, vervaardiger, prys.
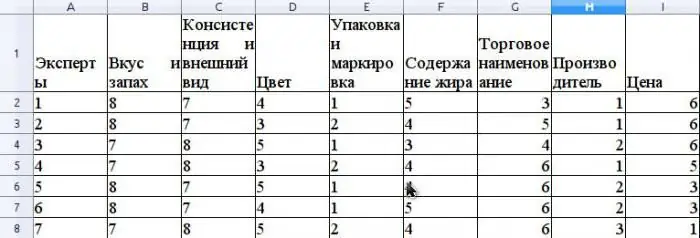
Veronderstel dat die kundige groep bestaan uit 7 kundiges. Die figuur toon die resultate van die rangorde van hierdie eiendomme.
Die gemiddelde waarde van r word bereken as die rekenkundige gemiddelde en sal 31,5 wees. Om S te vind, som die kwadraatverskille tussen ris en r-gemiddeld, volgens die formule hierbo, en bepaal dat die waarde van S 1718 is.
Bereken die konkordansiekoëffisiënt deur die formule te gebruik sonder om verwante range te gebruik (range sal verwant wees as dieselfde deskundige adviseur dieselfde range vir verskillende eienskappe gehad het).
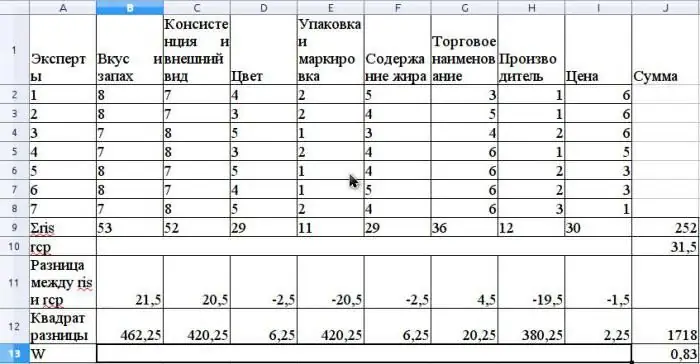
Die waarde van hierdie koëffisiënt sal 0.83 wees. Dit dui op 'n sterk konsensus onder kundiges.
Gaan die betekenis daarvan na deur die Pearson-toets te gebruik:
7 x 0,83 x (8-1)=40,7.
Pearson se tabeltoets op 1% betekenisvlak is 18.5, en op 5% - 14.1..
Die voorbeeld demonstreer die eenvoud en toeganklikheid van die berekening vir enige persoon wat die basiese beginsels van wiskundige berekeninge ken. Om hulle te verlig,gebruik sigbladvorms.
Ten slot
Die konkordansiekoëffisiënt toon dus die konsekwentheid van die menings van verskeie kundiges. Hoe verder dit van 0 af is en nader aan 1, hoe meer konsekwente menings. Hierdie koëffisiënte moet bevestig word deur die Pearson-kriterium te bereken.






