Daar is allerhande meganiese toestelle. Sommige van hulle is al van kleins af aan ons bekend. Dit is byvoorbeeld horlosies, fietse, tolle. Ons leer van ander soos ons ouer word. Dit is motors van motors, liere van hyskrane en ander. Elke bewegende meganisme gebruik een of ander stelsel om die wiele te laat draai en die masjien te laat werk. Een van die interessantste en gewildste is die planetêre meganisme. Die essensie daarvan lê daarin dat die masjien aangedryf word deur wiele of ratte wat op 'n spesiale manier met mekaar in wisselwerking tree. Kom ons bekyk dit van naderby.
Algemene inligting
Die planetêre rat en die planetêre meganisme word so genoem in analogie met ons sonnestelsel, wat voorwaardelik soos volg voorgestel kan word: in die middel is daar 'n "son" (die sentrale wiel in die meganisme). "Planete" (klein wiele of satelliete) beweeg daaromheen. Al hierdie dele in die planetêre rat het uitwendige tande. Die voorwaardelike sonnestelsel het 'n grens in sy deursnee. Roldit word in die planetêre meganisme deur 'n groot wiel of episiklus uitgevoer. Dit het ook tande, net interne. Die meeste van die werk in hierdie ontwerp word uitgevoer deur die draer, wat 'n hefboommeganisme is. Beweging kan op verskillende maniere uitgevoer word: óf die son sal draai, óf die episiklus, maar altyd saam met die satelliete.
Tydens die werking van die planetêre meganisme kan 'n ander ontwerp gebruik word, byvoorbeeld twee sonne, satelliete en 'n draer, maar sonder 'n episiklus. Nog 'n opsie is twee epicycles, maar sonder die son. Draer en satelliete moet altyd teenwoordig wees. Afhangende van die aantal wiele en die ligging van hul rotasie-asse in die ruimte, kan die ontwerp eenvoudig of kompleks, plat of ruimtelik wees.
Om ten volle te verstaan hoe so 'n stelsel werk, moet jy die besonderhede verstaan.
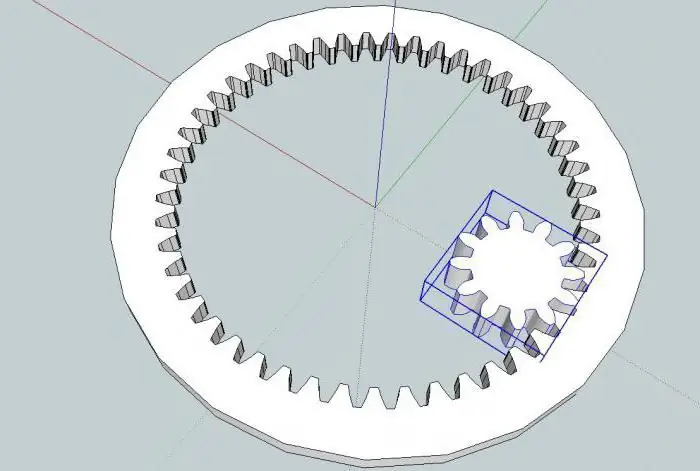
Ligging van elemente
Die eenvoudigste vorm van planetêre rat sluit drie stelle ratte met verskillende grade van vryheid in. Bogenoemde satelliete draai om hul asse en terselfdertyd om die son, wat in plek bly. Die episiklus verbind die planetêre meganisme van buite af en roteer ook deur middel van 'n alternatiewe koppeling van die tande (dit en die satelliete). Hierdie ontwerp is in staat om die wringkrag (hoeksnelhede) in een vlak te verander.
In 'n eenvoudige planetêre meganisme kan die son en satelliete draai, terwyl die episentrum vas bly. Die hoeksnelhede van alle komponente is in elk geval nie chaoties nie, maar het 'n lineêre afhanklikheid van mekaar. Soos die media roteer, verskaf ditlae spoed hoë wringkrag uitset.
Dit wil sê, die kern van die planetêre rat is dat so 'n ontwerp in staat is om te verander, uit te brei en wringkrag en hoeksnelheid by te voeg. Rotasiebewegings vind in hierdie geval in een meetkundige as plaas. Die nodige transmissie-element van verskeie voertuie en meganismes is geïnstalleer.

Kenmerke van strukturele materiale en skemas
'n vaste komponent is egter nie altyd nodig nie. In differensiële stelsels roteer elke element. Planetêre ratte soos hierdie een het een uitset aangedrewe (beheer) twee insette. Byvoorbeeld, 'n ewenaar wat 'n as in 'n motor beheer, is 'n soortgelyke rat.
Sulke stelsels werk op dieselfde beginsel as parallelle skagstrukture. Selfs 'n eenvoudige planeetrat het twee insette, die vaste ringrat is 'n konstante inset van nulhoeksnelheid.
Gedetailleerde beskrywing van toestelle
Gemengde planetêre strukture kan 'n ander aantal wiele hê, sowel as verskillende ratte waardeur hulle verbind word. Die teenwoordigheid van sulke besonderhede vergroot die moontlikhede van die meganisme aansienlik. Saamgestelde planetêre strukture kan saamgestel word sodat die as van die draerplatform teen hoë spoed beweeg. Gevolglik kan sommige probleme met reduksierat, sonrat en ander uitgeskakel word in die proses om die toestel te verbeter.
Dus, soos gesien vanuitgegewe inligting, werk die planetêre meganisme op die beginsel van die oordrag van rotasie tussen skakels wat sentraal en mobiel is. Terselfdertyd is komplekse stelsels meer in aanvraag as eenvoudiges.
Konfigurasie-opsies
Dit is moontlik om wiele (ratte) van verskeie konfigurasies in die planetêre meganisme te gebruik. Geskikte standaard met reguit tande, spiraalvormig, wurm, chevron. Die tipe inskakeling sal nie die algemene beginsel van werking van die planetêre meganisme beïnvloed nie. Die belangrikste ding is dat die rotasie-asse van die draer en die sentrale wiele saamval. Maar die asse van die satelliete kan in ander vlakke (kruising, parallel, kruisend) geleë wees. 'n Voorbeeld van gekruis is 'n tussenwielewenaar, waarin die ratte konies is. 'n Voorbeeld van gekruis is 'n selfsluitende ewenaar met 'n wurmrat (Torsen).
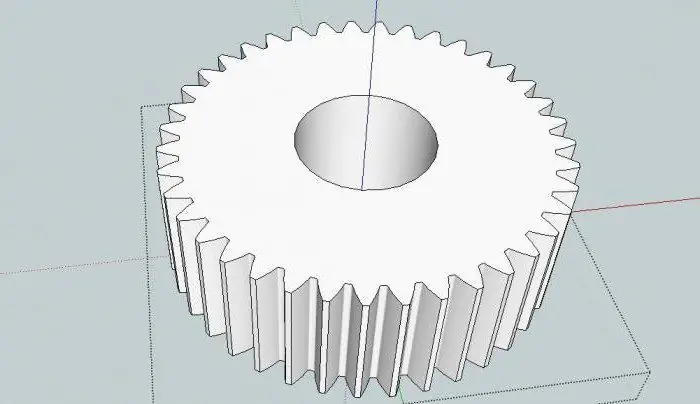
Eenvoudige en komplekse toestelle
Soos hierbo genoem, sluit die skema van die planetêre meganisme altyd 'n draer en twee sentrale wiele in. Daar kan enige aantal satelliete wees. Dit is die sogenaamde eenvoudige of elementêre toestel. In sulke meganismes kan ontwerpe soos volg wees: "SVS", "SVE", "EVE", waar:
- S is die son.
- B - draer.
- E is die episentrum.
Elke so 'n stel wiele + satelliete word 'n planetêre ratstel genoem. In hierdie geval moet alle wiele in dieselfde vlak draai. Eenvoudige meganismes is enkel- en dubbelry. Hulle word selde in verskeie tegniese toestelle en masjiene gebruik. N voorbeeldkan dien as 'n planetêre fietsmeganisme. Volgens hierdie beginsel werk die mou, waardeur die beweging uitgevoer word. Die ontwerp is volgens die "SVE"-skema geskep. Satelliete in nie 4 stukke nie. In hierdie geval is die son styf vas aan die as van die agterwiel, en die episentrum is beweegbaar. Dit word gedwing om te draai deur 'n fietsryer wat die pedale druk. In hierdie geval kan die transmissiespoed, en dus die rotasiespoed, verander.
Jy kan meer dikwels komplekse planetêre meganismes vind. Hul skemas kan baie verskil, wat afhang van waarvoor hierdie of daardie ontwerp bedoel is. As 'n reël bestaan komplekse meganismes uit verskeie eenvoudiges, geskep volgens die algemene reël vir 'n planetêre rat. Sulke komplekse stelsels is twee-, drie- of vierrye. Teoreties is dit moontlik om strukture met 'n groot aantal rye te skep, maar in die praktyk gebeur dit nie.
Planêre en ruimtelike toestelle
Sommige mense dink dat 'n eenvoudige planeetrat plat moet wees. Dit is net gedeeltelik waar. Komplekse toestelle kan ook plat wees. Dit beteken dat die planetêre ratte, maak nie saak hoeveel daarvan in die toestel gebruik word nie, in een of in parallelle vlakke is. Ruimtelike meganismes het planetêre ratte in twee of meer vlakke. In hierdie geval kan die wiele self kleiner wees as in die eerste uitvoering. Let daarop dat die plat planetêre meganisme dieselfde is as die ruimtelike een. Die verskil is slegs in die area wat deur die toestel beset word, dit wil sê in kompaktheid.
Grade van vryheid
Dit is die naam van die versamelingrotasie-koördinate, wat jou toelaat om die posisie van die stelsel in die ruimte op 'n gegewe tydstip te bepaal. Trouens, elke planetêre meganisme het ten minste twee grade van vryheid. Dit wil sê, die hoeksnelhede van rotasie van enige skakel in sulke toestelle is nie lineêr verwant, soos in ander ratte nie. Dit laat jou toe om by die uitsethoeksnelhede te kom wat nie dieselfde is as dié by die inset nie. Dit kan verklaar word deur die feit dat daar in die differensiële verbinding in die planetêre meganisme drie elemente in enige ry is, en die res sal lineêr daarmee verbind word, deur enige element van die ry. Teoreties is dit moontlik om planetêre stelsels met drie of meer grade van vryheid te skep. Maar in die praktyk is hulle onwerkbaar.

Planetêre ratverhouding
Dit is die belangrikste eienskap van rotasiebeweging. Dit laat jou toe om te bepaal hoeveel keer die kragmoment op die aangedrewe as toegeneem het in verhouding tot die oomblik van die dryfas. Jy kan die ratverhouding bepaal deur die formules te gebruik:
i=d2/d1=Z2/Z1=M2/M1=W1/W2=n1/n2, waar:
- 1 - voorste skakel.
- 2 - slaweskakel.
- d1, d2 - diameters van die eerste en tweede skakels.
- Z1, Z2 - aantal tande.
- M1, M2 is wringkragte.
- W1 W2 - hoeksnelhede.
- n1 n2 - spoed.
Dus, wanneer die ratverhouding hoër as een op die aangedrewe as is, neem die kragmoment toe, en die frekwensie en hoeksnelheid neem af. Dit moet altyd in ag geneem word wanneer 'n ontwerp geskep word, wantdie ratverhouding in planetêre meganismes hang af van hoeveel tande die wiele het, en watter element van die ry die voorste een is.
Omvang van toepassing
In vandag se wêreld is daar baie verskillende masjiene. Baie van hulle werk met die hulp van planetêre ratte.
Hulle word gebruik in motorewenaars, planetêre ratte, in die kinematiese skemas van komplekse masjiengereedskap, in vliegtuie se lugmotorratkaste, in fietse, in stropers en trekkers, in tenks en ander militêre toerusting. Volgens die beginsels van planetêre rat werk baie ratkaste in die aandrywings van elektriese kragopwekkers. Oorweeg nog so 'n stelsel.
Planetêre draairat
Hierdie ontwerp word in sommige trekkers, spoorvoertuie en tenks gebruik. 'n Eenvoudige diagram van die toestel word in die figuur hieronder getoon.
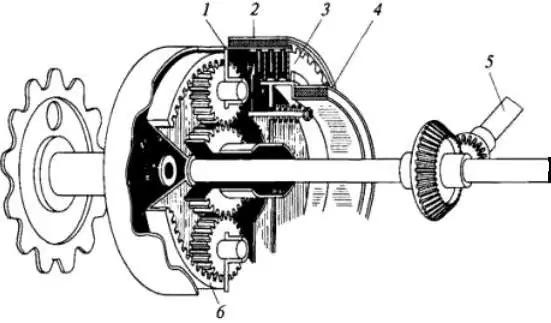
Die beginsel van werking van die planetêre rotasiemeganisme is soos volg: die draer (posisie 1) is gekoppel aan die remdrom (2) en die dryfwiel wat in die ruspe geleë is. Die episiklus (6) is aan die transmissie-as (posisie 5) gekoppel. Die son (8) is aan die koppelaarskyf (3) en die swaairemdrom (4) gekoppel. Wanneer die sluitkoppelaar ingeskakel is en die bandremme afgeskakel is, sal die satelliete nie draai nie. Hulle sal soos hefbome word, aangesien hulle deur middel van tande met die son (8) en die episiklus (6) verbind word. Daarom dwing hulle hulle en die draer om gelyktydig om 'n gemeenskaplike as te draai. In hierdie geval is die hoeksnelheid dieselfde.
Wanneer jy die sluitkoppelaar ontkoppel en die rem aansitdraai die son sal begin stop, en die satelliete sal begin om hul asse te beweeg. So skep hulle 'n oomblik op die draer en draai die dryfwiel van die ruspe.
Wear
In terme van lewensduur en demping, in lineêre planetêre stelsels, is die ladingverspreiding opmerklik tussen die hoofkomponente.
Termiese en sikliese moegheid kan in hulle toeneem as gevolg van die beperkte vragverspreiding en die feit dat planetêre ratte redelik vinnig om hul asse kan draai. Boonop kan sentrifugale kragte by hoë snelhede en ratverhoudings van die planetêre rat die hoeveelheid beweging aansienlik verhoog. Daar moet ook op gelet word dat namate die akkuraatheid van produksie afneem en die aantal satelliete toeneem, die neiging tot wanbalans toeneem.
Hierdie toestelle en hul stelsels kan selfs onderhewig wees aan slytasie. Sommige ontwerpe sal sensitief wees vir selfs klein wanbalanse en mag kwaliteit en duur samestelling komponente vereis. Die presiese ligging van die planetêre penne om die sonrat-as kan 'n sleutel wees.
Ander planetêre rangskikkings wat vragte help balanseer, sluit die gebruik van drywende subsamestellings of "sagte" monterings in om die son of episentrum so lank as moontlik te laat beweeg.

Grondbeginsels van sintese van planetêre toestelle
Hierdie kennis is nodig wanneer masjienkomponente ontwerp en geskep word. Die konsep van "sintese van planetêre meganismes" is om die aantal tande te berekenin die son, episentrum en satelliete. In hierdie geval moet 'n aantal voorwaardes nagekom word:
- Die ratverhouding moet gelyk wees aan die vasgestelde waarde.
- Rattande-inskakeling moet korrek wees.
- Dit is nodig om die belyning van die insetas en die uitsetas te verseker.
- Buurt vereis (satelliete mag nie met mekaar inmeng nie).
Ook, wanneer jy ontwerp, moet jy die afmetings van die toekomstige struktuur, sy gewig en doeltreffendheid in ag neem.
As die ratverhouding (n) gegee word, dan moet die aantal tande op die son (S) en op die planetêre ratte (P) voldoen aan die vergelyking:
n=S/P
As ons aanneem dat die aantal tande by die episentrum vroeg is (A), dan met die draer gesluit, moet die gelykheid waargeneem word:
n=-S/A
As die episentrum vas is, sal die volgende gelykheid waar wees:
n=1+ A/S
Dit is hoe die planetêre meganisme bereken word.

Voordele en nadele
Daar is verskeie tipes transmissie wat suksesvol in verskeie toestelle gebruik word. Planetêr onder hulle staan uit vir die volgende voordele:
- Verskaf minder las op elke tand van die wiele (beide die son, en die episentrum, en satelliete) as gevolg van die feit dat die las op hulle meer eweredig versprei word. Dit het 'n positiewe uitwerking op die lewensduur van die struktuur.
- Met dieselfde krag het die planeetrat kleiner afmetings en gewig as ander tipes transmissie.
- Vermoë om hoër ratverhoudings te bereik metminder wiele.
- Verseker minder geraas.
Nadele van planetêre ratte:
- Benodig meer akkuraatheid in hul vervaardiging.
- Lae doeltreffendheid met 'n relatief groot ratverhouding.






