Een van die hooftake van die ontleding van dinamiese beheerstelsels is die oplossing van die probleem van hul stabiliteit. Hul stabiliteit is een van die belangrikste kenmerke van die bestuurskonsep. Die stelsel word as onstabiel beskou as dit nie na sy oorspronklike posisie terugkeer nie, maar aanhou ossilleer nadat dit 'n paar veranderinge by die inset ondergaan het, of onder die invloed van 'n ongewenste versteuring is.
Definisie van die hoofbegrip
Volgens die konsep van stelselstabiliteit is die toestand van sy ewewig te wyte aan die afwesigheid van die impak van steurende faktore daarop. In hierdie situasie neig die verskil tussen die stel en werklike toestand na nul. Stabiliteit is sy vermoë om terug te keer na sy oorspronklike toestand van ewewig nadat die versteuring wat gelei het tot die skending daarvan geëindig het. 'n Onstabiele sisteem, as gevolg van die impak van 'n versteuring, beweeg weg van die ewewigstoestand of ossilleer, waarvan die amplitude geleidelikstyg.

Stabiliteitstoestande
Vir die stabiliteit van 'n stelsel met konstante tyd, moet die volgende twee voorwaardes nagekom word:
- Sy sal 'n beperkte uitset vir elke inset skep; as daar geen invoer is nie, moet die uitset nul wees, ongeag enige aanvanklike toestande.
- Die stabiliteit van die stelsel kan absolute of relatiewe stabiliteit genoem word. Die voorgestelde term word gebruik in verband met 'n studie waarin sekere hoeveelhede vergelyk word, hul bedryfstoestande. Stabiliteit is die eindresultaat wat deur die resultaat geskep word.
As die uitset van 'n stelsel oneindig is, selfs wanneer 'n eindige inset daarop toegepas word, sal gesê word dat dit onstabiel is, dit wil sê, inherent stabiel, dit het 'n begrensde terminasie wanneer 'n begrensde begin toegepas word op self.
In hierdie geval word die insette verstaan as verskeie toepassingspunte van die invloed van die eksterne omgewing op die stelsel. Die uitset is die finale produk van sy aktiwiteit, wat in die vorm van die getransformeerde insetdata is.
In 'n kontinue lineêre tydstelsel kan die stabiliteitstoestand vir 'n bepaalde impulsrespons geskryf word.
Wanneer dit diskreet is, kan die stabiliteitsindeks ook vir 'n bepaalde impulsrespons geskryf word.
Vir 'n onstabiele toestand in beide kontinue en begrensde sisteme, sal hierdie uitdrukkings oneindig wees.
tipes stabiliteit en steurnisse
Onder statiesDie stabiliteit van die stelsel word verstaan as sy vermoë om die herstel van die oorspronklike (of naby aan die oorspronklike) regime te verseker na 'n klein versteuring. Onder die konsep wat in hierdie konteks aangebied word, beskou hulle 'n fluktuasie wat sy gedrag beïnvloed, ongeag waar die oplewing of val voorkom, en wat die omvang daarvan is. Op grond hiervan laat hierdie modusse, wat naby aan die aanvanklike een is, ons dit as lineêr beskou.
Dynamiese stabiliteit van stelsels is die vermoë van laasgenoemde om die aanvanklike toestand na 'n groot versteuring te herstel.
Onder 'n groot fluktuasie word so 'n beweging verstaan, waarvan die aard van die invloed en die ooreenstemmende gedrag die tyd van bestaan, die grootte en plek van sy voorkoms bepaal.
Op grond hiervan word die stelsel in hierdie reeks gedefinieer as nie-lineêr.
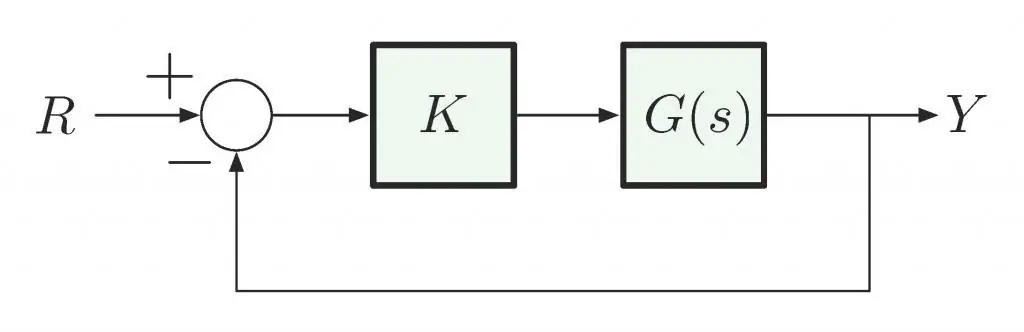
Kriteria vir die bepaling van volhoubaarheid
Die hoofvoorwaarde vir die stabiliteit van 'n lineêre stelsel is nie die aard van die versteuring nie, maar die struktuur daarvan. Daar word geglo dat hierdie stabiliteit "in die kleine" bepaal word as die grense daarvan nie vasgestel word nie. Stabiliteit "in die groot" word bepaal deur die perke en die ooreenstemming van werklike afwykings tot hierdie vasgestelde perke.
Om die stabiliteit van die stelsel te bepaal, word die volgende kriteria gebruik:
- wortelmaatstaf;
- Stodola-kriterium;
- Hurwitz-kriterium;
- Nyquist-kriterium;
- Mikhailov-kriterium en ander
Die wortelmaatstaf en Stodola se evalueringstegniek word gebruik om die stabiliteit van individuele skakels te bepaalen oop stelsels. Die Hurwitz-kriterium is algebraïes en laat toe om die stabiliteit van geslote sisteme sonder versuim te bepaal. Die Nyquist- en Mikhailov-kriteria is frekwensie-kriteria. Hulle word gebruik om die stabiliteit van geslote stelsels te bepaal op grond van hul frekwensierespons.

wortelmaatstaf
Dit laat jou toe om die stabiliteit van die stelsel te bepaal, gebaseer op die vorm van die oordragfunksie. Die gedragseienskappe daarvan word beskryf deur 'n kenmerkende polinoom (die noemer van die oordragfunksie). As ons die noemer aan nul gelykstel, sal die wortels van die resulterende vergelyking ons toelaat om die graad van stabiliteit te bepaal.
Volgens hierdie maatstaf sal die lineêre stelsel stabiel wees as al die wortels van die vergelyking in die linker halfvlak is. As ten minste een van hulle op die stabiliteitsgrens geleë is, sal dit ook by die limiet wees. As ten minste een van hulle in die regte halfvlak is, kan die stelsel as onstabiel beskou word.
Stodola-kriterium
Dit volg uit die worteldefinisie. In ooreenstemming met die Stodola-kriterium kan 'n lineêre stelsel as stabiel beskou word as alle koëffisiënte van die polinoom positief is.
Hurwitz-kriterium
Hierdie maatstaf word gebruik vir die kenmerkende polinoom van 'n geslote sisteem. Volgens hierdie tegniek is 'n voldoende voorwaarde vir stabiliteit die feit dat die waarde van die determinant en alle hoof diagonale minderjariges van die matriks groter as nul is. As ten minste een van hulle gelyk isnul, dit word op die stabiliteitsgrens beskou. As daar ten minste een negatiewe determinant is, moet dit as onstabiel beskou word.
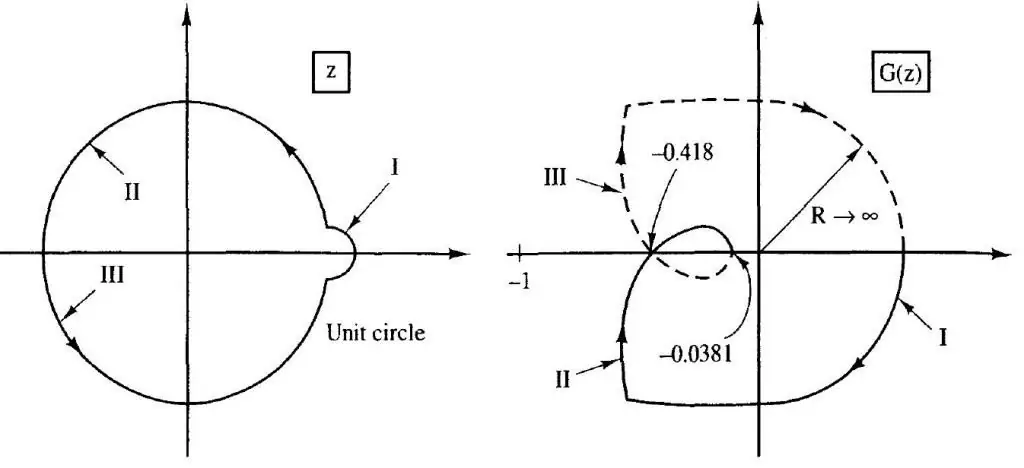
Nyquist-kriterium
Die basis van hierdie tegniek is die konstruksie van 'n kromme wat die punte van 'n vektor van 'n veranderlike verbind wat die oordragfunksie vertoon. Die formulering van die kriterium is soos volg: 'n geslote sisteem word as stabiel beskou as die funksiekromme nie 'n punt met koördinate (-1, j0) op die komplekse vlak insluit nie.
Finansiële gesonde stelsel
Finansiële veerkragtigheid is die toestand waarin die stelsel, dit wil sê sleutelmarkte en -instellings, bestand is teen ekonomiese skokke en gereed is om sy kernfunksies van kontantvloeibemiddeling, risikobestuur en betalingsreëlings glad te verrig.
As gevolg van die wedersydse afhanklikheidsverhouding van die verskaffing van interpretasie (beide vertikaal en horisontaal), moet die ontleding die hele finansiële bemiddelingstelsel dek. Met ander woorde, benewens die banksektor is dit ook nodig om nie-bankinstellings wat in een of ander vorm by bemiddeling betrokke is, te ontleed. Dit sluit talle soorte instellings in, insluitend makelaarsfirmas, beleggingsfondse, versekeraars en ander (verskeie) entiteite. Wanneer 'n stelsel van finansiële stabiliteit ontleed word, word die mate waarin die hele struktuur in staat is om eksterne en interne skokke te weerstaan, bestudeer. Skokke lei natuurlik nie altyd tot krisisse nie, maar die onstabiele finansiële omgewing selfop sy eie kan die gesonde ontwikkeling van die ekonomie belemmer.
Verskeie teorieë identifiseer die oorsake van finansiële onstabiliteit. Hul relevansie kan wissel na gelang van die tydperk en die lande wat by die omvang van die ontleding betrokke is. Onder die problematiese faktore wat die hele finansiële stelsel raak, identifiseer die literatuur gewoonlik die volgende:
- vinnige liberalisering van die finansiële sektor;
- onvoldoende ekonomiese beleid;
- Ongeteikende wisselkoersmeganisme;
- ondoeltreffende toewysing van hulpbronne;
- swak toesig;
- Onvoldoende regulering van rekeningkunde en ouditering.
Moontlike oorsake verskyn nie net gesamentlik nie, maar ook individueel of in 'n ewekansige kombinasie, dus is die ontleding van finansiële stabiliteit 'n uiters moeilike taak. Die fokus op individuele bedrywe verdraai die groot prentjie, daarom moet die kwessies in hul kompleksiteit oorweeg word in die loop van die bestudering van finansiële stabiliteit.

Die proses om die stabiliteit van die ondernemingstelsel te ontleed vind in verskeie stadiums plaas.
Aanvanklik word absolute en relatiewe aanwysers van finansiële stabiliteit geëvalueer en ontleed. In die tweede stadium word die faktore in ooreenstemming met hul betekenis verdeel, hul invloed word kwalitatief en kwantitatief beoordeel.
Finansiële sterkteverhoudings van ondernemings
Die finansiële toestand van die maatskappy, sy stabiliteit hang grootliks af van die optimale struktuur van kapitaalbronne, dit wil sê die verhouding van skuld tot eie hulpbronne, van die optimaledie struktuur van die maatskappy se bates en eerstens op die verhouding van vaste en bedryfsbates, asook die balans van fondse en laste van die maatskappy.
Daarom is dit belangrik om die struktuur van bronne van waagkapitaal te bestudeer en die mate van finansiële stabiliteit en risiko te bepaal. Vir hierdie doel word die koëffisiënte van stelselstabiliteit gebruik:
- koëffisiënt van outonomie (onafhanklikheid) - die aandeel van kapitaal in die balansstaat;
- afhanklikheidsverhouding - die aandeel van geleende kapitaal in die balansstaat;
- lopende skuldverhouding - die verhouding van korttermyn finansiële laste tot die balansstaat;
- finansiële stabiliteitsverhouding (langtermyn finansiële onafhanklikheid) - die verhouding van kapitaal en langtermynskuld tot die balansstaat;
- skulddekkingsverhouding (solvensieverhouding) - die verhouding van kapitaal tot skuld;
- finansiële hefboomverhouding (finansiële risikoverhouding) - die verhouding van skuld tot kapitaal.

Hoe hoër die vlak van aanwysers soos outonomie, finansiële stabiliteit, dekking van skuldkapitaal, hoe laer is die vlak van 'n ander groep koëffisiënte (afhanklikheid, huidige skuld, langtermynverpligtinge teenoor beleggers) en dienooreenkomstig die stabiliteit van die maatskappy se finansiële toestand. Finansiële hefboomfinansiering word ook finansiële hefboomfinansiering genoem.






