Die onderwerp van ons vandag se artikel sal die kinematika van 'n wesenlike punt wees. Waaroor gaan dit alles? Watter konsepte kom daarin voor en watter definisie moet aan hierdie term gegee word? Ons sal vandag probeer om hierdie en baie ander vrae te beantwoord.
Definisie en konsep
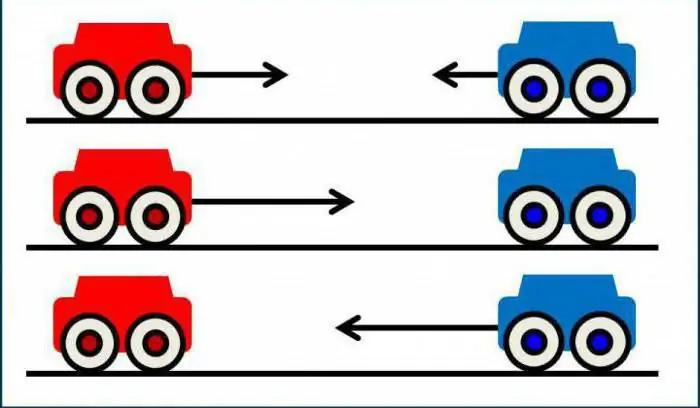
Kinematika van 'n materiële punt is niks meer as 'n onderafdeling van fisika wat "meganika" genoem word nie. Sy bestudeer op haar beurt die bewegingspatrone van sekere liggame. Die kinematika van 'n materiële punt handel ook oor hierdie probleem, maar doen dit nie op 'n algemene manier nie. Trouens, hierdie onderafdeling bestudeer metodes wat jou toelaat om die beweging van liggame te beskryf. In hierdie geval is slegs die sogenaamde geïdealiseerde liggame geskik vir navorsing. Dit sluit in: 'n materiaalpunt, 'n absoluut stewige liggaam en 'n ideale gas. Kom ons kyk na die konsepte in meer detail. Ons weet almal van die skoolbank af dat dit gebruiklik is om 'n materiële punt 'n liggaam te noem, waarvan die afmetings in 'n gegewe situasie afgeskeep kan word. Terloops, die kinematika van die translasiebeweging van 'n materiële punt begin vir die eerste keerverskyn in graad sewende fisika handboeke. Dit is die eenvoudigste tak, so dit is die gerieflikste om met sy hulp kennis te maak met die wetenskap. 'n Aparte vraag is wat die elemente van die kinematika van 'n materiële punt is. Daar is nogal baie van hulle, en voorwaardelik kan hulle verdeel word in verskeie vlakke met verskillende kompleksiteit vir begrip. As ons byvoorbeeld praat oor die radiusvektor, dan is daar in beginsel niks buitengewoon ingewikkeld in sy definisie nie. U sal egter saamstem dat dit vir 'n student baie makliker sal wees om dit te verstaan as vir 'n student van middel- of hoërskool. En om eerlik te wees, is dit nie nodig om die kenmerke van hierdie kwartaal aan hoërskoolleerlinge te verduidelik nie.
'n Kort geskiedenis van die skepping van kinematika
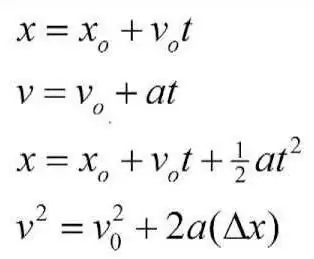
Baie, baie jare gelede het die groot wetenskaplike Aristoteles die grootste deel van sy vrye tyd aan die studie en beskrywing van fisika as 'n aparte wetenskap gewy. Hy het ook aan kinematika gewerk en probeer om die hoofteses en konsepte daarvan aan te bied, op een of ander manier gebruik in pogings om praktiese en selfs alledaagse probleme op te los. Aristoteles het die aanvanklike idees gegee oor wat die elemente van die kinematika van 'n materiële punt is. Sy werke en werke is baie waardevol vir die hele mensdom. Nietemin het hy in sy gevolgtrekkings 'n aansienlike aantal foute gemaak, en die rede hiervoor was sekere wanopvattings en wanberekeninge. Op 'n tyd het 'n ander wetenskaplike, Galileo Galilei, in die werke van Aristoteles begin belangstel. Een van die fundamentele stellings wat Aristoteles voorgehou het, was dat die beweging van 'n liggaamvind slegs plaas as dit deur een of ander krag, bepaal deur intensiteit en rigting, daarop ingewerk word. Galileo het bewys dat dit 'n fout was. Die krag sal die bewegingspoedparameter beïnvloed, maar nie meer nie. Die Italianer het gewys dat krag die oorsaak van versnelling is, en dit kan net wedersyds daarmee ontstaan. Galileo Galilei het ook aansienlike aandag gegee aan die studie van die proses van vrye val, deur die toepaslike patrone af te lei. Waarskynlik onthou almal sy beroemde eksperimente, wat hy op die Leunende Toring van Pisa uitgevoer het. Die fisikus Ampère het ook die basiese beginsels van kinematiese oplossings in sy werke gebruik.
Aanvanklike konsepte
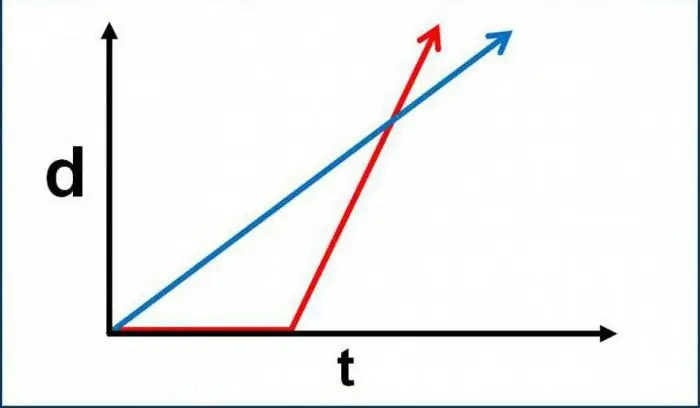
Soos vroeër genoem, is kinematika die studie van maniere om die beweging van geïdealiseerde voorwerpe te beskryf. In hierdie geval kan die basiese beginsels van wiskundige analise, gewone algebra en meetkunde in die praktyk toegepas word. Maar watter konsepte (juis konsepte, en nie definisies vir parametriese hoeveelhede nie) lê onder hierdie onderafdeling van fisika? Eerstens moet almal duidelik verstaan dat die kinematika van die translasiebeweging van 'n materiële punt beweging in ag neem sonder om kragaanwysers in ag te neem. Dit wil sê, om die ooreenstemmende probleme op te los, het ons nie formules nodig wat met krag verband hou nie. Dit word nie deur kinematika in ag geneem nie, maak nie saak hoeveel van hulle daar is nie - een, twee, drie, ten minste 'n paar honderdduisend. Nietemin word die bestaan van versnelling steeds verskaf. In 'n aantal probleme skryf die kinematika van die beweging van 'n materiaalpunt voor om die grootte van die versnelling te bepaal. Die oorsake van hierdie verskynsel (dit is die kragte enhul aard) word nie oorweeg nie, maar weggelaat.
Klassifikasie
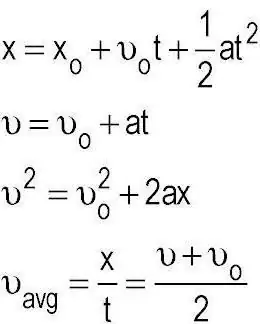
Ons het uitgevind dat kinematika metodes ondersoek en toepas om die beweging van liggame te beskryf sonder inagneming van die kragte wat op hulle inwerk. Terloops, 'n ander onderafdeling van meganika, wat dinamika genoem word, handel oor so 'n taak. Reeds daar word Newton se wette toegepas, wat dit in die praktyk toelaat om heelwat parameters met 'n klein hoeveelheid bekende aanvanklike data te bepaal. Die basiese konsepte van die kinematika van 'n materiële punt is ruimte en tyd. En in verband met die ontwikkeling van die wetenskap sowel in die algemeen as op hierdie gebied, het die vraag ontstaan oor die toepaslikheid van die gebruik van so 'n kombinasie.
Van die begin af was daar klassieke kinematika. Ons kan sê dat dit nie net gekenmerk word deur die teenwoordigheid van beide tydelike en ruimtelike gapings nie, maar ook hul onafhanklikheid van die keuse van een of ander verwysingsraamwerk. Terloops, ons sal 'n bietjie later hieroor praat. Kom ons verduidelik nou net waarvan ons praat. In hierdie geval sal 'n segment as 'n ruimtelike interval beskou word, en 'n tydinterval sal as 'n temporele interval beskou word. Alles blyk duidelik te wees. So, hierdie gapings sal in klassieke kinematika beskou word as absoluut, onveranderlik, met ander woorde, onafhanklik van die oorgang van een verwysingsraamwerk na 'n ander. Of besigheid relativistiese kinematika. Daarin kan die gapings tydens die oorgang tussen verwysingstelsels verander. Dit sal selfs meer korrek wees om te sê dat hulle nie kan nie, maar hulle moet, waarskynlik. As gevolg hiervan, die gelyktydigheid van die tweeewekansige gebeure word ook relatief en onderhewig aan spesiale oorweging. Dit is hoekom in relativistiese kinematika twee konsepte - ruimte en tyd - in een gekombineer word.
Kinematika van 'n materiaalpunt: spoed, versnelling en ander hoeveelhede
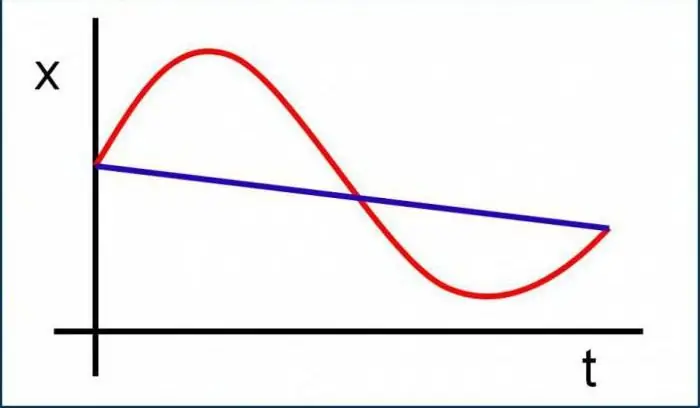
Om ten minste 'n bietjie hierdie onderafdeling van fisika te verstaan, moet jy deur die belangrikste konsepte navigeer, die definisies ken en jou voorstel wat hierdie of daardie hoeveelheid in algemene terme is. Daar is niks moeilik hierin nie, om die waarheid te sê, alles is baie maklik en eenvoudig. Oorweeg miskien om mee te begin die basiese konsepte wat in kinematiese probleme gebruik word.
Beweging
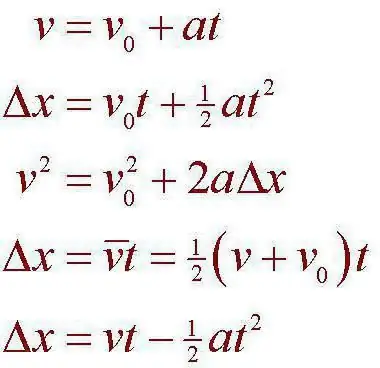
Meganiese beweging ons sal die proses oorweeg waartydens een of ander geïdealiseerde voorwerp sy posisie in die ruimte verander. In hierdie geval kan ons sê dat die verandering plaasvind relatief tot ander liggame. Dit is ook nodig om die feit in ag te neem dat die vasstelling van 'n sekere tydsinterval tussen twee gebeurtenisse gelyktydig plaasvind. Dit sal byvoorbeeld moontlik wees om 'n sekere interval wat gevorm word gedurende die tyd wat verloop het tussen die liggaam se aankoms van een posisie na 'n ander te isoleer. Ons neem ook kennis dat die liggame in hierdie geval met mekaar kan en sal interaksie hê, volgens die algemene wette van meganika. Dit is presies waarmee die kinematika van 'n materiaalpunt die meeste werk. Die verwysingsisteem is die volgende konsep wat onlosmaaklik daarmee verbind is.
Koördinate
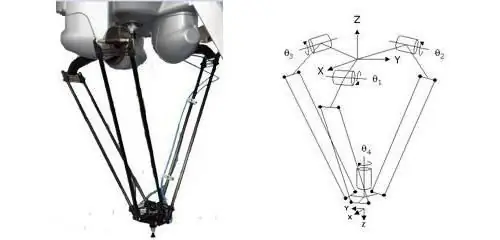
Hulle kan gewone data genoem word wat jou toelaat om die posisie van die liggaam een of ander tyd te bepaal. Koördinate is onlosmaaklik verbind met die konsep van 'n verwysingstelsel, sowel as die koördinaatrooster. Meestal is dit 'n kombinasie van letters en syfers.
Radiusvektor
Uit die naam behoort dit reeds duidelik te wees wat dit is. Nietemin, laat ons hieroor in meer detail praat. As 'n punt langs 'n sekere trajek beweeg, en ons ken presies die begin van 'n spesifieke verwysingstelsel, dan kan ons enige tyd 'n radiusvektor teken. Dit sal die beginposisie van die punt aan die oombliklike of finale posisie verbind.
Trajectory
Dit sal 'n aaneenlopende lyn genoem word, wat gelê word as gevolg van die beweging van 'n materiaalpunt in 'n spesifieke verwysingstelsel.
Speed (beide lineêr en hoekig)
Dit is 'n waarde wat kan sê hoe vinnig die liggaam deur 'n bepaalde afstand-interval gaan.
Versnelling (beide hoek en lineêr)
Wys volgens watter wet en hoe intensief die spoedparameter van die liggaam verander.
Miskien, hier is hulle - die hoofelemente van die kinematika van 'n materiële punt. Daar moet kennis geneem word dat beide snelheid en versnelling vektorhoeveelhede is. En dit beteken dat hulle nie net een of ander aanduidingswaarde het nie, maar ook 'n sekere rigting. Terloops, hulle kan beide in een rigting en in teenoorgestelde rigtings gerig word. In die eerste geval sal die liggaam versnel, in die tweede sal dit stadiger word.
Eenvoudige take
Kinematika van 'n materiële punt (snelheid, versnelling en afstand waarin prakties fundamentele konsepte is) sluit nie net 'n groot aantal take in nie, maar baie van hul verskillende kategorieë. Kom ons probeer om 'n redelik eenvoudige probleem op te los deur die afstand te bepaal wat die liggaam afgelê het.
Gestel die voorwaardes wat ons het, is soos volg. Die bestuurder se motor is by die wegspringlyn. Die operateur gee die trekpas met die vlag, en die motor vat skielik op. Bepaal of sy 'n nuwe rekord in die kompetisie van renjaers kan opstel, as die volgende leier 'n afstand van honderd meter in 7,8 sekondes afgelê het. Neem die versnelling van die motor gelyk aan 3 meter gedeel deur 'n tweede kwadraat.
So, hoe om hierdie probleem op te los? Dit is nogal interessant, aangesien daar van ons verwag word om nie sekere parameters te "droog" te bepaal nie. Dit word opgehelder met omset en 'n sekere situasie, wat die proses van oplossing en soek na aanwysers diversifiseer. Maar waardeur moet ons gelei word voordat ons die taak aanpak?
1. Die kinematika van 'n materiaalpunt maak voorsiening vir die gebruik van versnelling in hierdie geval.
2. Die oplossing word aangeneem deur die afstandsformule te gebruik, aangesien die numeriese waarde daarvan in die toestande verskyn.
Die probleem is eintlik eenvoudig opgelos. Om dit te doen, neem ons die afstandsformule: S=VoT + (-) AT ^ 2/2. Wat is die punt? Ons moet uitvind hoe lank die ruiter die aangewese afstand sal aflê, en dan die syfer met die rekord vergelyk om uit te vind of hy dit klop of nie. Om dit te doen, ken tyd toe, ons kry die formulevir hom: AT^2 + 2VoT - 2S. Dit is niks meer as 'n kwadratiese vergelyking nie. Maar die motor styg op, wat beteken dat die aanvanklike spoed 0 sal wees. Wanneer die vergelyking opgelos word, sal die diskriminant gelyk wees aan 2400. Om die tyd te vind, moet jy die wortel skiet. Kom ons doen dit tot die tweede desimale plek: 48.98. Vind die wortel van die vergelyking: 48.98/6=8.16 sekondes. Dit blyk dat die bestuurder nie die bestaande rekord sal kan klop nie.






