Wanneer die eienskappe van 'n kwadratiese vergelyking bestudeer is, is 'n beperking gestel - vir 'n diskriminant minder as nul is daar geen oplossing nie. Daar is dadelik bepaal dat ons van 'n stel reële getalle praat. Die nuuskierige verstand van 'n wiskundige sal belangstel - wat is die geheim vervat in die klousule oor werklike waardes?
Wiskundiges het met verloop van tyd die konsep van komplekse getalle bekendgestel, waar die voorwaardelike waarde van die tweede wortel van minus een as 'n eenheid geneem word.
Historiese agtergrond
Wiskundige teorie ontwikkel opeenvolgend, van eenvoudig tot kompleks. Kom ons vind uit hoe die konsep genaamd "komplekse getal" ontstaan het en hoekom dit nodig is.
Van ouds af was die basis van wiskunde die gewone rekening. Die navorsers het net die natuurlike stel waardes geken. Optelling en aftrekking was eenvoudig. Namate ekonomiese verhoudings meer kompleks geword het, het vermenigvuldiging begin gebruik word in plaas van om dieselfde waardes by te voeg. Daar is 'n omgekeerde bewerking omvermenigvuldiging - deling.
Die konsep van 'n natuurlike getal het die gebruik van rekenkundige bewerkings beperk. Dit is onmoontlik om alle deelprobleme op die stel heelgetalwaardes op te los. Werk met breuke het eers gelei tot die konsep van rasionele waardes, en toe tot irrasionele waardes. As dit vir die rasionale moontlik is om die presiese ligging van die punt op die lyn aan te dui, dan is dit vir die irrasionele onmoontlik om so 'n punt aan te dui. Jy kan net die interval benader. Die vereniging van rasionale en irrasionale getalle het 'n reële versameling gevorm, wat as 'n sekere lyn met 'n gegewe skaal voorgestel kan word. Elke stap langs die lyn is 'n natuurlike getal, en tussen hulle is rasionale en irrasionele waardes.
Die era van teoretiese wiskunde het begin. Die ontwikkeling van sterrekunde, meganika, fisika het die oplossing van meer en meer komplekse vergelykings vereis. Oor die algemeen is die wortels van die kwadratiese vergelyking gevind. By die oplossing van 'n meer komplekse kubiese polinoom het wetenskaplikes 'n teenstrydigheid teëgekom. Die konsep van 'n derdemagswortel uit 'n negatief maak sin, maar vir 'n vierkantswortel word onsekerheid verkry. Boonop is die kwadratiese vergelyking slegs 'n spesiale geval van die kubieke een.
In 1545 het die Italianer J. Cardano voorgestel om die konsep van 'n denkbeeldige getal bekend te stel.

Hierdie getal is die tweede wortel van minus een. Die term komplekse getal is uiteindelik eers driehonderd jaar later gevorm, in die werke van die beroemde wiskundige Gauss. Hy het voorgestel om al die wette van algebra formeel uit te brei na die denkbeeldige getal. Die regte lyn is uitgebrei navliegtuie. Die wêreld is groter.
Basiese konsepte
Onthou 'n aantal funksies wat beperkings op die werklike stel het:
- y=arcsin(x), gedefinieer tussen negatief en positief 1.
- y=ln(x), desimale logaritme maak sin met positiewe argumente.
- vierkantswortel y=√x, slegs bereken vir x ≧ 0.
Om i=√(-1) aan te dui, stel ons so 'n konsep in as 'n denkbeeldige getal, dit sal alle beperkings van die definisiedomein van bogenoemde funksies verwyder. Uitdrukkings soos y=arcsin(2), y=ln(-4), y=√(-5) maak sin in een of ander spasie van komplekse getalle.
Die algebraïese vorm kan geskryf word as 'n uitdrukking z=x + i×y op die stel reële x- en y-waardes, en i2 =-1.
Die nuwe konsep verwyder alle beperkings op die gebruik van enige algebraïese funksie en lyk soos 'n grafiek van 'n reguit lyn in koördinate van werklike en denkbeeldige waardes.
Komplekse vliegtuig
Die meetkundige vorm van komplekse getalle stel ons visueel in staat om baie van hul eienskappe voor te stel. Op die Re(z)-as merk ons die werklike x-waardes, op die Im(z) - die denkbeeldige waardes van y, dan sal die z-punt op die vlak die vereiste komplekse waarde vertoon.
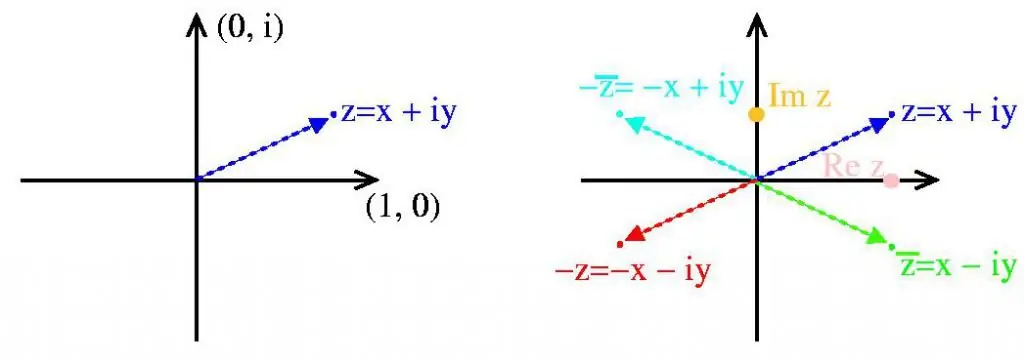
Definisies:
- Re(z) - regte as.
- Im(z) - beteken die denkbeeldige as.
- z - voorwaardelike punt van 'n komplekse getal.
- Die numeriese waarde van die lengte van die vektor van nul tot z word genoemmodule.
- Regte en denkbeeldige asse verdeel die vliegtuig in kwarte. Met 'n positiewe waarde van die koördinate - ek kwartaal. Wanneer die argument van die reële as minder as 0 is, en die denkbeeldige as is groter as 0 - II kwart. Wanneer die koördinate negatief is - III kwart. Die laaste, vierde kwartaal bevat baie positiewe reële waardes en negatiewe denkbeeldige waardes.
Dus, op 'n vlak met x- en y-koördinaatwaardes, kan 'n mens altyd 'n punt van 'n komplekse getal visualiseer. Die karakter i word bekendgestel om die werklike deel van die denkbeeldige een te skei.
Properties
- Wanneer die waarde van die denkbeeldige argument nul is, kry ons net 'n getal (z=x), wat op die reële as geleë is en tot die reële versameling behoort.
- Spesiale geval wanneer die waarde van die werklike argument nul word, stem die uitdrukking z=i×y ooreen met die ligging van die punt op die denkbeeldige as.
- Die algemene vorm van z=x + i×y sal vir nie-nul waardes van die argumente wees. Dui die ligging van die punt aan wat die komplekse getal in een van die kwartale kenmerk.
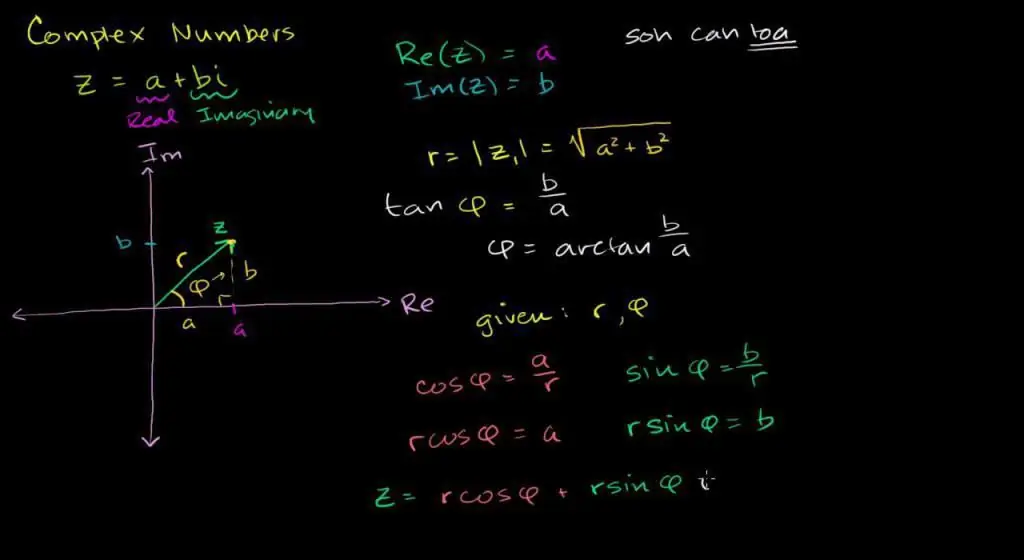
Trigonometriese notasie
Onthou die poolkoördinaatstelsel en die definisie van die trigonometriese funksies sin en cos. Dit is duidelik dat met behulp van hierdie funksies dit moontlik is om die ligging van enige punt op die vliegtuig te beskryf. Om dit te doen, is dit genoeg om die lengte van die poolbundel en die hellingshoek tot die werklike as te ken.
Definisie. 'n Inskrywing van die vorm ∣z ∣ vermenigvuldig met die som van die trigonometriese funksies cos(ϴ) en die denkbeeldige deel i ×sin(ϴ) word 'n trigonometriese komplekse getal genoem. Hier is die benaming die hellingshoek tot die reële as
ϴ=arg(z) en r=∣z∣, balklengte.
Uit die definisie en eienskappe van trigonometriese funksies volg 'n baie belangrike Moivre-formule:
zn =r × (cos(n × ϴ) + i × sin(n × ϴ)).
Deur hierdie formule te gebruik, is dit gerieflik om baie stelsels vergelykings op te los wat trigonometriese funksies bevat. Veral wanneer die probleem van verheffing tot 'n mag ontstaan.
Module en fase
Om die beskrywing van 'n komplekse stel te voltooi, stel ons twee belangrike definisies voor.
Om die Pythagoras-stelling te ken, is dit maklik om die lengte van die bundel in die poolkoördinaatstelsel te bereken.
r=∣z∣=√(x2 + y2), so 'n notasie op 'n komplekse spasie word 'n " genoem module" en karakteriseer die afstand van 0 na 'n punt op die vliegtuig.
Die hellingshoek van die komplekse straal na die reële lyn ϴ word algemeen die fase genoem.
Die definisie toon dat die werklike en denkbeeldige dele met behulp van sikliese funksies beskryf word. Naamlik:
- x=r × cos(ϴ);
- y=r × sin(ϴ);
Omgekeerd, die fase hou verband met algebraïese waardes deur die formule:
ϴ=arctan(x / y) + µ, korreksie µ word ingestel om die periodisiteit van meetkundige funksies in ag te neem.
Euler-formule
Wiskundiges gebruik dikwels die eksponensiële vorm. Komplekse vliegtuiggetalle word as uitdrukkings geskryf
z=r × ei×ϴ , wat volg uit die Euler-formule.

Hierdie rekord word wyd gebruik vir die praktiese berekening van fisiese hoeveelhede. Vorm van aanbieding in die vormeksponensiële komplekse getalle is veral gerieflik vir ingenieursberekeninge, waar dit nodig word om stroombane met sinusvormige strome te bereken en dit is nodig om die waarde van integrale van funksies met 'n gegewe tydperk te ken. Die berekeninge self dien as 'n hulpmiddel in die ontwerp van verskeie masjiene en meganismes.
Definieer bewerkings
Soos reeds opgemerk, is alle algebraïese wette van werk met basiese wiskundige funksies van toepassing op komplekse getalle.
Sombewerking
Wanneer komplekse waardes bygevoeg word, word hul werklike en denkbeeldige dele ook bygevoeg.
z=z1 + z2 waar z1 en z2 - algemene komplekse getalle. Deur die uitdrukking te transformeer, nadat ons die hakies oopgemaak en die notasie vereenvoudig het, kry ons die werklike argument x=(x1 + x2), die denkbeeldige argument y=(y 1 + y2).
Op die grafiek lyk dit soos die byvoeging van twee vektore, volgens die bekende parallelogramreël.
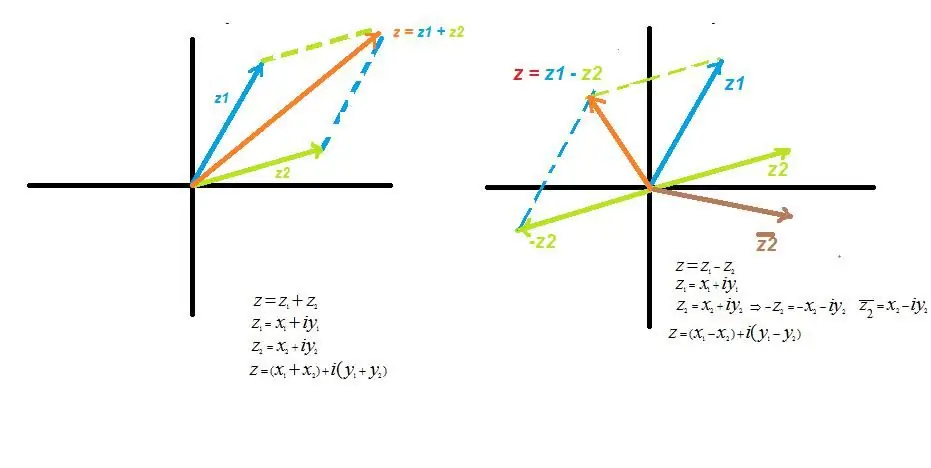
Aftrekbewerking
Beskou as 'n spesiale geval van optelling, wanneer een getal positief is, is die ander negatief, dit wil sê, geleë in die spieëlkwartier. Algebraïese notasie lyk soos die verskil tussen werklike en denkbeeldige dele.
z=z1 - z2, of, met inagneming van die waardes van die argumente, soortgelyk aan die byvoeging bewerking, kry ons vir die reële waardes x=(x1 - x2) en denkbeeldige y=(y1- y2).
Vermenigvuldiging op die komplekse vlak
Deur die reëls te gebruik om met polinome te werk, lei ons die formule afom komplekse getalle op te los.
Volg die algemene algebraïese reëls z=z1×z2, beskryf elke argument en lys soortgelykes. Die werklike en denkbeeldige dele kan soos volg geskryf word:
- x=x1 × x2 - y1 × y2,
- y=x1 × y2 + x2 × y 1.
Dit lyk mooier as ons eksponensiële komplekse getalle gebruik.
Die uitdrukking lyk soos volg: z=z1 × z2 =r1 × eiϴ1 × r2 × eiϴ2=r1 × r2 × ei(ϴ1+ϴ2).
Verder eenvoudig, die modules word vermenigvuldig en die fases word bygevoeg.
Division
Wanneer ons die werking van deling as die inverse van vermenigvuldiging oorweeg, kry ons 'n eenvoudige uitdrukking in eksponensiële notasie. Deur die waarde z1 deur z2 te deel is die resultaat van die verdeling van hul modules en faseverskil. Formeel, wanneer die eksponensiële vorm van komplekse getalle gebruik word, lyk dit soos volg:
z=z1 / z2 =r1 × e iϴ1 / r2 × ei ϴ2=r1 / r2× ei(ϴ1-ϴ 2).
In die vorm van algebraïese notasie word die bewerking van die verdeling van die getalle van die komplekse vlak effens meer ingewikkeld geskryf:
z=z1 / z2.
Deur argumente te beskryf en polinoomtransformasies uit te voer, is dit maklik om waardes te kryx=x1 × x2 + y1 × y2, onderskeidelik y=x2 × y1 - x1 × y2 , binne die beskryfde ruimte, maak hierdie uitdrukking egter sin as z2 ≠ 0.
Uittrek die wortel
Al die bogenoemde kan toegepas word wanneer meer komplekse algebraïese funksies gedefinieer word - verhoog tot enige mag en omgekeerd daaraan - onttrek die wortel.
Deur die algemene konsep van verhoging tot die mag n te gebruik, kry ons die definisie:
zn =(r × eiϴ).
Gebruik algemene eienskappe, herskryf as:
zn =rn × eiϴ.
Ons het 'n eenvoudige formule gekry om 'n komplekse getal tot 'n mag te verhoog.
Uit die definisie van die graad kry ons 'n baie belangrike gevolg. 'n Ewe mag van die denkbeeldige eenheid is altyd 1. Enige onewe mag van die denkbeeldige eenheid is altyd -1.
Kom ons bestudeer nou die omgekeerde funksie - onttrek die wortel.
Vir gemak van notasie, kom ons neem n=2. Die vierkantswortel w van die komplekse waarde z op die komplekse vlak C word beskou as die uitdrukking z=±, geldig vir enige werklike argument groter as of gelyk aan nul. Vir w ≦ 0 is daar geen oplossing nie.
Kom ons kyk na die eenvoudigste kwadratiese vergelyking z2 =1. Gebruik komplekse getalformules, herskryf r2 × ei2ϴ =r2 × ei2ϴ=ei0. Dit kan uit die rekord gesien word dat r2 =1 en ϴ=0, daarom het ons 'n unieke oplossing gelyk aan 1. Maar dit weerspreek die idee dat z=-1 ook by die definisie van 'n vierkantswortel pas.
Kom ons vind uit wat ons nie in ag neem nie. As ons die trigonometriese notasie herroep, dan herstel ons die stelling - met 'n periodieke verandering in die fase ϴ, verander die komplekse getal nie. Laat p die waarde van die periode aandui, dan het ons r2 × ei2ϴ =ei(0+p), waarvandaan 2ϴ=0 + p, of ϴ=p / 2. Daarom, ei0 =1 en eip/2 =-1. Ons het die tweede oplossing gekry, wat ooreenstem met die algemene begrip van die vierkantswortel.
Dus, om 'n arbitrêre wortel van 'n komplekse getal te vind, sal ons die prosedure volg.
- Skryf die eksponensiële vorm w=∣w∣ × ei(arg (w) + pk), k is 'n arbitrêre heelgetal.
- Die verlangde getal word ook voorgestel in die Euler-vorm z=r × eiϴ.
- Gebruik die algemene definisie van die wortelekstraksiefunksie r ei ϴ =∣w∣ × ei(arg(w) + pk).
- Uit die algemene eienskappe van die gelykheid van modules en argumente skryf ons rn =∣w∣ en nϴ=arg (w) + p×k.
- Die finale rekord van die wortel van 'n komplekse getal word beskryf deur die formule z=√∣w∣ × ei ( arg (w) + pk ) / .
- Let wel. Die waarde van ∣w∣, per definisie,is 'n positiewe reële getal, so die wortel van enige graad maak sin.
Veld en vervoeging
Ten slotte gee ons twee belangrike definisies wat van min belang is vir die oplossing van toegepaste probleme met komplekse getalle, maar noodsaaklik is vir die verdere ontwikkeling van wiskundige teorie.
Daar word gesê dat die uitdrukkings vir optelling en vermenigvuldiging 'n veld vorm as hulle voldoen aan die aksiomas vir enige elemente van die komplekse vlak z:
- Die komplekse som verander nie van veranderende plekke van komplekse terme nie.
- Die stelling is waar - in 'n komplekse uitdrukking kan enige som van twee getalle deur hul waarde vervang word.
- Daar is 'n neutrale waarde 0 waarvoor z + 0=0 + z=z waar is.
- Vir enige z is daar 'n teenoorgestelde - z, bytelling wat nul gee.
- Wanneer die plek van komplekse faktore verander word, verander die komplekse produk nie.
- Die vermenigvuldiging van enige twee getalle kan deur hul waarde vervang word.
- Daar is 'n neutrale waarde 1, vermenigvuldiging waarmee nie die komplekse getal verander nie.
- Vir elke z ≠ 0 is daar 'n inverse van z-1, wat vermenigvuldig met 1.
- Om die som van twee getalle met 'n derde te vermenigvuldig is gelykstaande aan die bewerking om elkeen van hulle met hierdie getal te vermenigvuldig en die resultate by te tel.
- 0 ≠ 1.
Die getalle z1 =x + i×y en z2 =x - i×y word vervoeg.
Stelling. Vir vervoeging is die stelling waar:
- Die vervoeging van die som is gelyk aan die som van vervoegde elemente.
- Die vervoeging van die produk isproduk van vervoegings.
- Die vervoeging van vervoeging is gelyk aan die getal self.
In die algemeen algebra word sulke eienskappe veld-outomorfismes genoem.
Voorbeelde
Deur die gegewe reëls en formules van komplekse getalle te volg, kan jy maklik daarmee werk.
Kom ons kyk na die eenvoudigste voorbeelde.
Probleem 1. Gebruik die vergelyking 3y +5 x i=15 - 7i, bepaal x en y.
Besluit. Herinner die definisie van komplekse gelykhede, dan is 3y=15, 5x=-7. Daarom, x=-7 / 5, y=5.
Taak 2. Bereken die waardes 2 + i28 en 1 + i135.
Besluit. Uiteraard is 28 'n ewe getal, uit die gevolg van die definisie van 'n komplekse getal in die mag het ons i28 =1, wat beteken dat die uitdrukking 2 + i 28 =3. Die tweede waarde, i135 =-1, dan 1 + i135 =0.
Taak 3. Bereken die produk van die waardes 2 + 5i en 4 + 3i.
Besluit. Uit die algemene eienskappe van vermenigvuldiging van komplekse getalle verkry ons (2 + 5i)X(4 + 3i)=8 - 15 + i(6 + 20). Die nuwe waarde sal -7 + 26i wees.
Taak 4. Bereken die wortels van die vergelyking z3 =-i.
Besluit. Daar is verskeie maniere om 'n komplekse getal te vind. Kom ons kyk na een van die moontlike. Per definisie, ∣ - i∣=1, is die fase vir -i -p / 4. Die oorspronklike vergelyking kan herskryf word as r3ei3ϴ =e-p/4+pk, van waar z=e-p / 12 + pk/3, vir enige heelgetal k.
Die oplossingstel het die vorm (e-ip/12,eip/4, ei2 p/3).
Hoekom het ons komplekse getalle nodig
Geskiedenis ken baie voorbeelde wanneer wetenskaplikes, wat aan 'n teorie werk, nie eers aan die praktiese toepassing van hul resultate dink nie. Wiskunde is eerstens 'n spel van die verstand, 'n streng nakoming van oorsaak-en-gevolg verhoudings. Byna alle wiskundige konstruksies word gereduseer tot die oplossing van integraal- en differensiaalvergelykings, en dié word op hul beurt, met 'n mate van benadering, opgelos deur die wortels van polinome te vind. Hier kom ons eers die paradoks van denkbeeldige getalle teë.
Wetenskaplikes natuurkundiges, wat heeltemal praktiese probleme oplos, hul wending tot oplossings van verskeie vergelykings, ontdek wiskundige paradokse. Die interpretasie van hierdie paradokse lei tot absoluut wonderlike ontdekkings. Die dubbele aard van elektromagnetiese golwe is een so 'n voorbeeld. Komplekse getalle speel 'n deurslaggewende rol om hul eienskappe te verstaan.
Dit het op sy beurt praktiese toepassing gevind in optika, radio-elektronika, energie en baie ander tegnologiese velde. Nog 'n voorbeeld, baie moeiliker om fisiese verskynsels te verstaan. Antimaterie is op die punt van 'n pen voorspel. En eers baie jare later begin pogings om dit fisies te sintetiseer.
Moenie dink dat daar net in fisika sulke situasies is nie. Nie minder interessante ontdekkings word gemaak in die natuurlewe, in die sintese van makromolekules, tydens die studie van kunsmatige intelligensie nie. En dit is alles te danke aanuitbreiding van ons bewussyn, wegbeweeg van eenvoudige optelling en aftrekking van natuurlike waardes.






