Resolusie is die vermoë van 'n beeldstelsel om die besonderhede van 'n voorwerp weer te gee, en hang af van faktore soos die tipe beligting wat gebruik word, die pixelgrootte van die sensor en die vermoëns van die optika. Hoe kleiner die detail van die onderwerp, hoe hoër is die vereiste resolusie van die lens.
Inleiding tot die resolusieproses
Die beeldkwaliteit van die kamera hang af van die sensor. Eenvoudig gestel, 'n digitale beeldsensor is 'n skyfie in 'n kameraliggaam wat miljoene ligsensitiewe kolle bevat. Die grootte van 'n kamera se sensor bepaal hoeveel lig gebruik kan word om 'n beeld te skep. Hoe groter die sensor, hoe beter is die beeldkwaliteit namate meer inligting ingesamel word. Tipies adverteer digitale kameras in die mark vir sensorgroottes van 16 mm, Super 35 mm, en soms tot 65 mm.
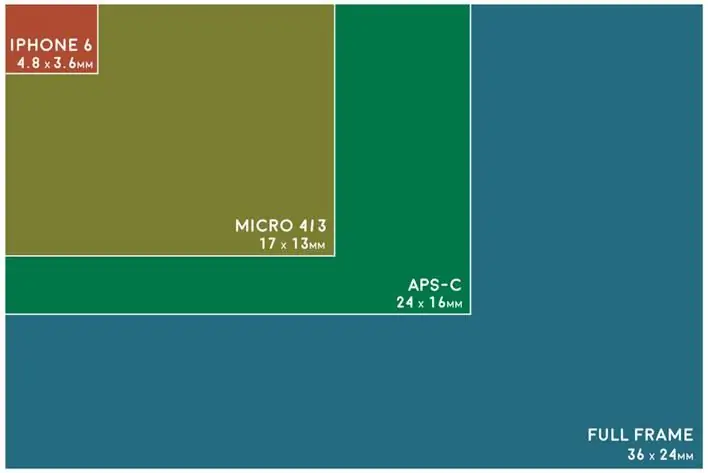
Soos die grootte van die sensor toeneem, sal die diepte van veld by 'n gegewe diafragma afneem, aangesien 'n groter eweknie vereis dat jy nader aanvoorwerp of gebruik 'n langer brandpunt om die raam te vul. Om dieselfde diepte van veld te handhaaf, moet die fotograaf kleiner diafragma's gebruik.
Hierdie vlak diepte van veld kan wenslik wees, veral om agtergrondvervaagdheid vir portrette te verkry, maar landskapfotografie vereis meer diepte, wat makliker is om vas te vang met die buigsame diafragmagrootte van kompakte kameras.
Die verdeling van die aantal horisontale of vertikale pieksels op 'n sensor sal aandui hoeveel spasie elkeen op 'n voorwerp beslaan, en kan gebruik word om lensoplossingskrag te evalueer en klante se kommer oor die toestel se digitale beeldpikselgrootte op te los. As 'n beginpunt is dit belangrik om te verstaan wat eintlik die stelsel se resolusie kan beperk.
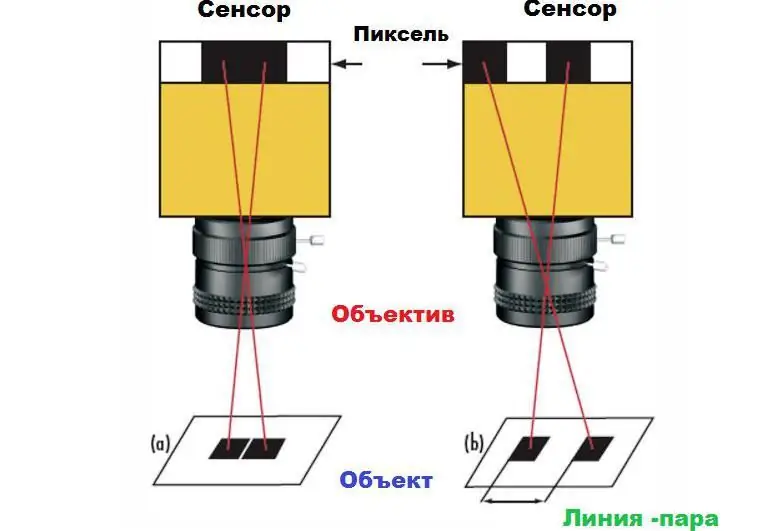
Hierdie stelling kan gedemonstreer word deur die voorbeeld van 'n paar blokkies op 'n wit agtergrond. As die vierkante op die kamerasensor gekarteer word na naburige pixels, sal hulle as een groot reghoek in die prent (1a) verskyn eerder as twee afsonderlike vierkante (1b). Om die blokkies te onderskei, word 'n sekere spasie tussen hulle vereis, ten minste een pixel. Hierdie minimum afstand is die maksimum resolusie van die stelsel. Die absolute limiet word bepaal deur die grootte van die pieksels op die sensor, sowel as hul getal.
Meetlenseienskappe
Die verwantskap tussen afwisselende swart en wit blokkies word beskryf as 'n lineêre paar. Tipies word resolusie bepaal deur frekwensie,gemeet in lynpare per millimeter - lp/mm. Ongelukkig is lensresolusie in cm nie 'n absolute getal nie. By 'n gegewe resolusie sal die vermoë om die twee vierkante as aparte voorwerpe te sien afhang van die grysskaalvlak. Hoe groter die grysskaal-skeiding tussen hulle en ruimte is, hoe meer stabiel is die vermoë om hierdie vierkante op te los. Hierdie verdeling van die grys skaal staan bekend as frekwensiekontras.
Ruimtelike frekwensie word gegee in lp/mm. Om hierdie rede is die berekening van resolusie in terme van lp/mm uiters nuttig wanneer lense vergelyk word en die beste keuse vir gegewe sensors en toepassings bepaal word. Die eerste een is waar die stelselresolusieberekening begin. Om met die sensor te begin, is dit makliker om te bepaal watter lensspesifikasies nodig is om aan die vereistes van die toestel of ander toepassings te voldoen. Die hoogste frekwensie wat deur die sensor, Nyquist, toegelaat word, is effektief twee pixels of een lynpaar.
Definisie lensresolusie, ook genoem stelselbeeldruimteresolusie, kan bepaal word deur die grootte in Μm met 2 te vermenigvuldig om 'n paar te skep en deur 1000 te deel om na mm: om te skakel
lp/mm=1000/ (2 X pixel)
Sensore met groter pixels sal laer resolusielimiete hê. Sensors met kleiner pieksels sal beter presteer volgens die lensresolusieformule hierbo.
Aktiewe sensorarea
Jy kan die maksimum resolusie vir die voorwerp berekenbesigtiging. Om dit te doen, is dit nodig om te onderskei tussen aanwysers soos die verhouding tussen die grootte van die sensor, die gesigsveld en die aantal pixels op die sensor. Die grootte van laasgenoemde verwys na die parameters van die aktiewe area van die kamerasensor, gewoonlik bepaal deur die grootte van sy formaat.
Die presiese verhoudings sal egter volgens aspekverhouding verskil, en nominale sensorgroottes moet slegs as 'n riglyn gebruik word, veral vir telesentriese lense en hoë vergrotings. Die sensorgrootte kan direk uit die piekselgrootte en aktiewe aantal pieksels bereken word om lensresolusietoets uit te voer.
Die tabel toon die Nyquist-limiet wat verband hou met pixelgroottes wat op sommige baie algemeen gebruikte sensors gevind word.
| Pikselgrootte (µm) | Gekoppelde Nyquist-limiet (lp / mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
Namate piekselgroottes afneem, neem die gepaardgaande Nyquist-limiet in lp/mm proporsioneel toe. Om die absolute minimum oplosbare kol wat op 'n voorwerp gesien kan word te bepaal, moet die verhouding van die gesigsveld tot die grootte van die sensor bereken word. Dit staan ook bekend as primêre aanvulling.(PMAG) stelsels.
Die verhouding wat met die stelsel PMAG geassosieer word, maak dit moontlik om die beeldruimte-resolusie te skaal. Tipies, wanneer 'n toepassing ontwerp word, word dit nie in lp/mm gespesifiseer nie, maar eerder in mikrons (µm) of breuke van 'n duim. Jy kan vinnig na die uiteindelike resolusie van 'n voorwerp spring deur die formule hierbo te gebruik om dit makliker te maak om die lensresolusie z te kies. Dit is ook belangrik om in gedagte te hou dat daar baie bykomende faktore is, en die bogenoemde beperking is baie minder foutgevoelig as die kompleksiteit van die inagneming van baie faktore en die berekening daarvan deur gebruik te maak van vergelykings.
Bereken brandpunt
Die resolusie van 'n prent is die aantal pixels daarin. Aangewys in twee dimensies, byvoorbeeld, 640X480. Berekeninge kan afsonderlik vir elke dimensie gedoen word, maar vir eenvoud word dit dikwels tot een verminder. Om akkurate metings op 'n prent te maak, moet jy 'n minimum van twee pixels gebruik vir elke kleinste area wat jy wil bespeur. Die grootte van die sensor verwys na 'n fisiese aanwyser en word as 'n reël nie in die paspoortdata aangedui nie. Die beste manier om die grootte van 'n sensor te bepaal, is om na die pixelparameters daarop te kyk en dit met die aspekverhouding te vermenigvuldig, in welke geval die oplosvermoë van die lens die probleme van 'n slegte skoot oplos.
Byvoorbeeld, die Basler acA1300-30um-kamera het 'n pixelgrootte van 3,75 x 3,75um en 'n resolusie van 1296 x 966 piksels. Die sensorgrootte is 3,75 µm x 1296 by 3,75 µm x 966=4,86 x 3,62 mm.
Sensorformaat verwys na die fisiese grootte en hang nie van die piekselgrootte af nie. Hierdie instelling word gebruik virbepaal met watter lens die kamera versoenbaar is. Vir hulle om te pas, moet die lensformaat groter as of gelyk aan die sensorgrootte wees. As 'n lens met 'n kleiner aspekverhouding gebruik word, sal die beeld vignettering ervaar. Dit veroorsaak dat areas van die sensor buite die rand van die lensformaat donker word.
Piksels en kamerakeuse

Om die voorwerpe in die prent te sien, moet daar genoeg spasie tussen hulle wees sodat hulle nie met naburige pixels saamsmelt nie, anders sal hulle nie van mekaar onderskei kan word nie. As die voorwerpe een pixel elk is, moet die skeiding tussen hulle ook ten minste een element wees, dit is te danke daaraan dat 'n paar lyne gevorm word, wat eintlik twee pixels groot het. Dit is een van die redes waarom dit verkeerd is om die resolusie van kameras en lense in megapixels te meet.
Dit is eintlik makliker om die resolusievermoëns van 'n stelsel in terme van lynpaarfrekwensie te beskryf. Dit volg dat soos die piekselgrootte afneem, die resolusie toeneem omdat jy kleiner voorwerpe op kleiner digitale elemente kan plaas, minder spasie tussen hulle kan hê, en steeds die afstand tussen die onderwerpe wat jy neem, kan oplos.
Dit is 'n vereenvoudigde model van hoe die kamera se sensor voorwerpe opspoor sonder om geraas of ander parameters in ag te neem, en is die ideale situasie.
MTF-kontraskaarte
Die meeste lense is nie perfekte optiese stelsels nie. Lig wat deur 'n lens gaan, ondergaan 'n sekere mate van agteruitgang. Die vraag is hoe om dit te evalueeragteruitgang? Voordat hierdie vraag beantwoord word, is dit nodig om die konsep van "modulasie" te definieer. Laasgenoemde is 'n maatstaf van die kontras len by 'n gegewe frekwensie. Mens kan probeer om werklike wêreldbeelde wat deur 'n lens geneem is te ontleed om modulasie of kontras te bepaal vir besonderhede van verskillende groottes of frekwensies (spasiëring), maar dit is baie onprakties.
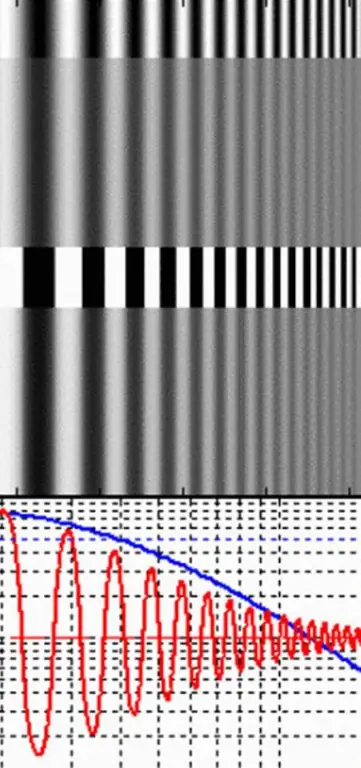
In plaas daarvan is dit baie makliker om modulasie of kontras te meet vir pare afwisselende wit en donker lyne. Hulle word reghoekige rooster genoem. Die interval van lyne in 'n reghoekige golfrooster is die frekwensie (v), waarvoor die modulasie- of kontrasfunksie van die lens en die resolusie in cm gemeet word.
Die maksimum hoeveelheid lig sal van die ligbande af kom, en die minimum van die donker bande. As lig gemeet word in terme van helderheid (L), kan die modulasie volgens die volgende vergelyking bepaal word:
modulasie=(Lmaks - Lmin) / (Lmaks + Lmin), waar: Lmax is die maksimum helderheid van wit lyne in die rooster, en Lmin is die minimum helderheid van donkers.
Wanneer modulasie in terme van lig gedefinieer word, word daar dikwels na verwys as Michelson-kontras omdat dit die verhouding van helderheid van lig en donker bande neem om kontras te meet.
Byvoorbeeld, daar is 'n vierkantgolfrooster van 'n sekere frekwensie (v) en modulasie, en 'n inherente kontras tussen donker en ligte areas wat vanaf hierdie rooster deur die lens gereflekteer word. Beeldmodulasie en dus lenskontras word gemeet vir 'n gegewe frekwensiemate (v).
Die modulasie-oordragfunksie (MTF) word gedefinieer as die modulasie M i van die beeld gedeel deur die modulasie van die stimulus (voorwerp) M o, soos getoon in die volgende vergelyking.
|
MTF (v)=M i / M 0 |
USF-toetsroosters word op 98% helder laserpapier gedruk. Swart laserdrukkertoner het 'n weerkaatsing van ongeveer 10%. Die waarde vir M 0 is dus 88%. Maar aangesien film 'n meer beperkte dinamiese omvang het in vergelyking met die menslike oog, is dit veilig om te aanvaar dat M 0 in wese 100% of 1 is. Die bogenoemde formule kom dus meer op die volgende neer eenvoudige vergelyking:
|
MTF (v)=Mi |
Dus die MTF-lens vir 'n gegewe roosterfrekwensie (v) is bloot die gemete roostermodulasie (Mi) wanneer dit deur 'n lens op film gefotografeer word.
Mikroskoopresolusie
Die resolusie van 'n mikroskoop-objektief is die kortste afstand tussen twee afsonderlike punte in sy oogstukveld wat steeds as verskillende voorwerpe onderskei kan word.
As twee punte nader aan mekaar is as jou resolusie, sal hulle vaag lyk en hul posisies sal onakkuraat wees. Die mikroskoop bied dalk hoë vergroting, maar as die lense van swak geh alte is, sal die gevolglike swak resolusie die beeldkwaliteit verswak.
Hieronder is die Abbe-vergelyking, waar die resolusieDie z-lenskrag van 'n mikroskoop is die oplosvermoë gelyk aan die golflengte van die lig wat gebruik word gedeel deur 2 (die numeriese diafragma van die objektief).
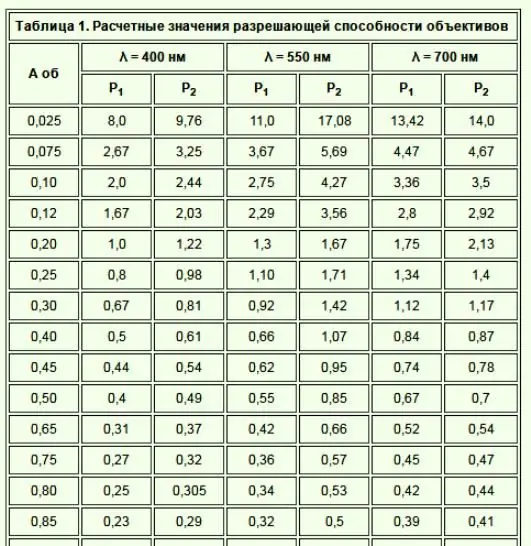
Verskeie elemente beïnvloed die resolusie van 'n mikroskoop. 'n Optiese mikroskoop wat op hoë vergroting gestel is, kan 'n beeld produseer wat vaag is, maar dit is steeds op die maksimum resolusie van die lens.
Die digitale diafragma van 'n lens beïnvloed resolusie. Die oplosvermoë van 'n mikroskoop-objektief is 'n getal wat die vermoë van 'n lens aandui om lig te versamel en 'n punt op 'n vaste afstand van die objektief op te los. Die kleinste punt wat deur die lens opgelos kan word, is eweredig aan die golflengte van die versamelde lig gedeel deur die numeriese diafragmanommer. Daarom stem 'n groter getal ooreen met 'n groter vermoë van die lens om 'n uitstekende punt in die gesigsveld op te spoor. Die numeriese diafragma van die lens hang ook af van die hoeveelheid optiese aberrasiekorreksie.
Resolusie van die teleskooplens
Soos 'n lig tregter, is 'n teleskoop in staat om lig in verhouding tot die area van die gat te versamel, hierdie eienskap is die hooflens.
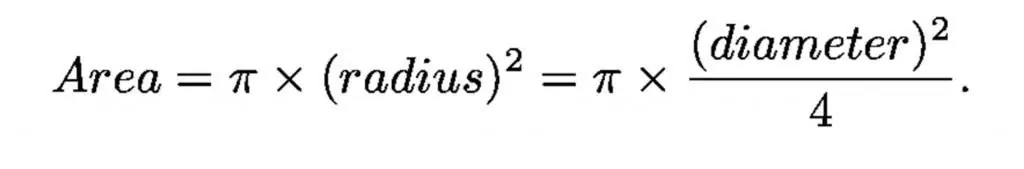
Die deursnee van die donker aangepaste pupil van die menslike oog is net minder as 1 sentimeter, en die deursnee van die grootste optiese teleskoop is 1 000 sentimeter (10 meter), sodat die grootste teleskoop een miljoen keer groter is in versameling area as die menslike oog.

Dit is hoekom teleskope dowwer voorwerpe as mense sien. En het toestelle wat lig opgaar deur elektroniese opsporingsensors vir baie ure te gebruik.
Daar is twee hooftipes teleskoop: lensgebaseerde refraktors en spieëlgebaseerde reflektors. Groot teleskope is weerkaatsers omdat spieëls nie deursigtig hoef te wees nie. Teleskoopspieëls is van die mees presiese ontwerpe. Die toegelate fout op die oppervlak is ongeveer 1/1000 die breedte van 'n menslike haar - deur 'n 10 meter gat.
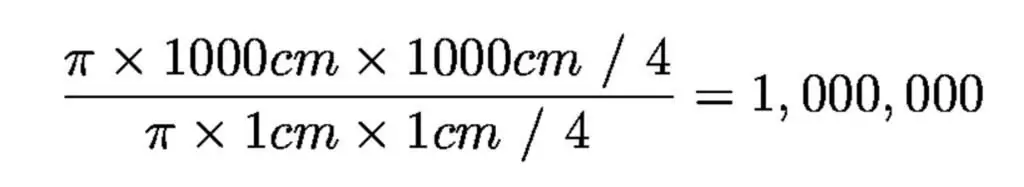
Spieëls was vroeër van groot dik glasplate gemaak om te keer dat hulle sak. Vandag se spieëls is dun en buigsaam, maar word rekenaarbeheer of andersins gesegmenteer en in lyn gebring deur rekenaarbeheer. Benewens die taak om dowwe voorwerpe te vind, is die sterrekundige se doel ook om hul fyn besonderhede te sien. Die mate waarin besonderhede herken kan word, word resolusie genoem:
- Fuzzy beelde=swak resolusie.
- Duidelike beelde=goeie resolusie.
As gevolg van die golfaard van lig en verskynsels wat diffraksie genoem word, beperk die deursnee van 'n teleskoop se spieël of lens sy uiteindelike resolusie relatief tot die deursnee van die teleskoop. Die resolusie hier beteken die kleinste hoekige detail wat herken kan word. Klein waardes stem ooreen met uitstekende beelddetail.
Radioteleskope moet baie groot wees om goeie resolusie te verskaf. Aarde se atmosfeer isonstuimige en vervaag teleskoopbeelde. Terrestriële sterrekundiges kan selde die maksimum resolusie van die apparaat bereik. Die onstuimige effek van die atmosfeer op 'n ster word visie genoem. Hierdie onstuimigheid laat die sterre “fonkel”. Om hierdie atmosferiese waas te vermy, lanseer sterrekundiges teleskope die ruimte in of plaas dit op hoë berge met stabiele atmosferiese toestande.
Voorbeelde van parameterberekening
Data om Canon-lensresolusie te bepaal:
- Pikselgrootte=3,45 µm x 3,45 µm.
- Piksels (H x V)=2448 x 2050.
- Gewenste gesigsveld (horisontaal)=100 mm.
- Sensorresolusielimiet: 1000/2x3, 45=145 lp/mm.
- Sensorafmetings:3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Meetlensresolusie: 145 x 0,0845=12,25 lp/mm.
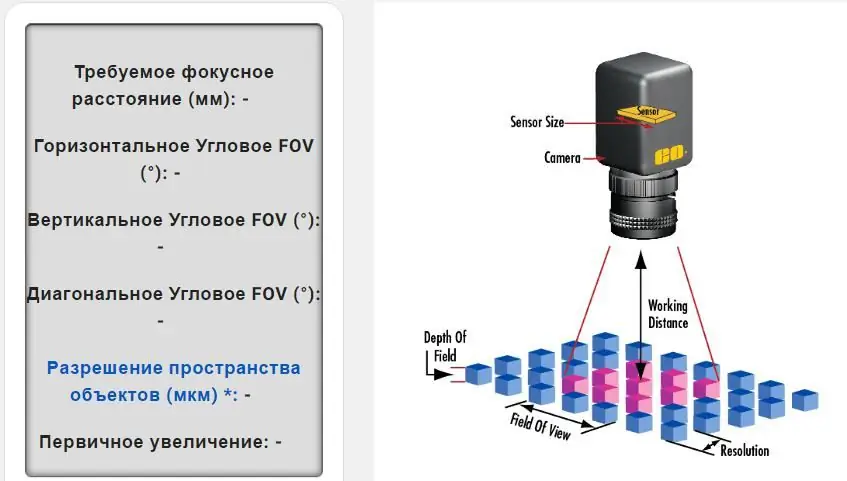
Eintlik is hierdie berekeninge redelik kompleks, maar hulle sal jou help om 'n beeld te skep wat gebaseer is op sensorgrootte, pixelformaat, werkafstand en gesigsveld in mm. Die berekening van hierdie waardes sal die beste lens vir jou beelde en toepassing bepaal.
Probleme van moderne optika

Ongelukkig skep die verdubbeling van die grootte van die sensor bykomende probleme vir lense. Een van die belangrikste parameters wat die koste van 'n beeldlens beïnvloed, is die formaat. Die ontwerp van 'n lens vir 'n groter formaat sensor vereistalle individuele optiese komponente, wat groter moet wees en die oordrag van die stelsel meer rigied.
'n Lens wat ontwerp is vir 'n 1"-sensor kan vyf keer soveel kos as 'n lens wat ontwerp is vir 'n ½"-sensor, selfs al kan dit nie dieselfde spesifikasies met beperkte piekselresolusie gebruik nie. Die koste-komponent moet oorweeg word voor hoe om die oplosvermoë van 'n lens te bepaal.
Optiese beelding staar vandag meer uitdagings in die gesig as 'n dekade gelede. Die sensors waarmee hulle gebruik word, het baie hoër resolusievereistes, en formaatgroottes word gelyktydig kleiner en groter aangedryf, terwyl pixelgrootte aanhou krimp.
In die verlede het optika nooit die beeldstelsel beperk nie, vandag is dit wel. Waar 'n tipiese pixelgrootte ongeveer 9 µm is, is 'n baie meer algemene grootte ongeveer 3 µm. Hierdie 81x toename in puntdigtheid het sy tol geëis op optika, en hoewel die meeste toestelle goed is, is lenskeuse nou belangriker as ooit.






