Modulus van elastisiteit is 'n fisiese grootheid wat die elastiese gedrag van 'n materiaal kenmerk wanneer 'n eksterne krag in 'n bepaalde rigting daarop toegepas word. Die elastiese gedrag van 'n materiaal beteken sy vervorming in die elastiese gebied.
Geskiedenis van die studie van elastisiteit van materiale

Die fisiese teorie van elastiese liggame en hul gedrag onder die werking van eksterne kragte is in detail oorweeg en bestudeer deur die Engelse wetenskaplike van die 19de eeu, Thomas Young. Die konsep van elastisiteit is egter in 1727 deur die Switserse wiskundige, fisikus en filosoof Leonhard Euler ontwikkel, en die eerste eksperimente met betrekking tot die elastisiteitsmodulus is in 1782 uitgevoer, dit wil sê 25 jaar voor die werk van Thomas Jung., deur die Venesiese wiskundige en filosoof Jacopo Ricatti.
Thomas Young se verdienste lê in die feit dat hy die teorie van elastisiteit 'n skraal moderne voorkoms gegee het, wat daarna geformaliseer is in die vorm van 'n eenvoudige en toe veralgemeende Hooke se wet.
Fisiese aard van elastisiteit
Enige liggaam bestaan uit atome, waartussen die kragte van aantrekking en afstoting inwerk. Die balans van hierdie kragte isdie toestand en parameters van materie onder gegewe toestande. Die atome van 'n soliede liggaam, wanneer onbeduidende eksterne kragte van spanning of kompressie op hulle toegepas word, begin verskuif, wat 'n krag teenoorgestelde in rigting en ewe groot is, wat geneig is om die atome na hul aanvanklike toestand terug te keer.
In die proses van so 'n verplasing van atome, neem die energie van die hele sisteem toe. Eksperimente toon dat by klein vervormings die energie eweredig is aan die kwadraat van hierdie vervormings. Dit beteken dat die krag, synde 'n afgeleide met betrekking tot energie, eweredig blyk te wees aan die eerste krag van die vervorming, dit wil sê, dit hang lineêr daarvan af. Deur die vraag te beantwoord, wat die elastisiteitsmodulus is, kan ons sê dat dit die koëffisiënt van proporsionaliteit is tussen die krag wat op die atoom inwerk en die vervorming wat hierdie krag veroorsaak. Die dimensie van Young se modulus is dieselfde as die dimensie van druk (Pascal).
Elastiese limiet
Volgens die definisie dui die elastisiteitsmodulus aan hoeveel spanning op 'n vaste stof toegepas moet word sodat sy vervorming 100% kan wees. Alle vaste stowwe het egter 'n elastiese limiet gelykstaande aan 1% vervorming. Dit beteken dat as 'n gepaste krag toegepas word en die liggaam vervorm word met 'n hoeveelheid minder as 1%, dan herstel die liggaam na die beëindiging van hierdie krag presies sy oorspronklike vorm en afmetings. As te veel krag toegepas word, waarteen die vervormingswaarde 1% oorskry, na die beëindiging van die eksterne krag, sal die liggaam nie meer sy oorspronklike afmetings herstel nie. In laasgenoemde geval word gepraat van die bestaan van 'n oorblywende vervorming, wat isbewys dat die elastiese limiet van die materiaal oorskry is.
Young se modulus in aksie
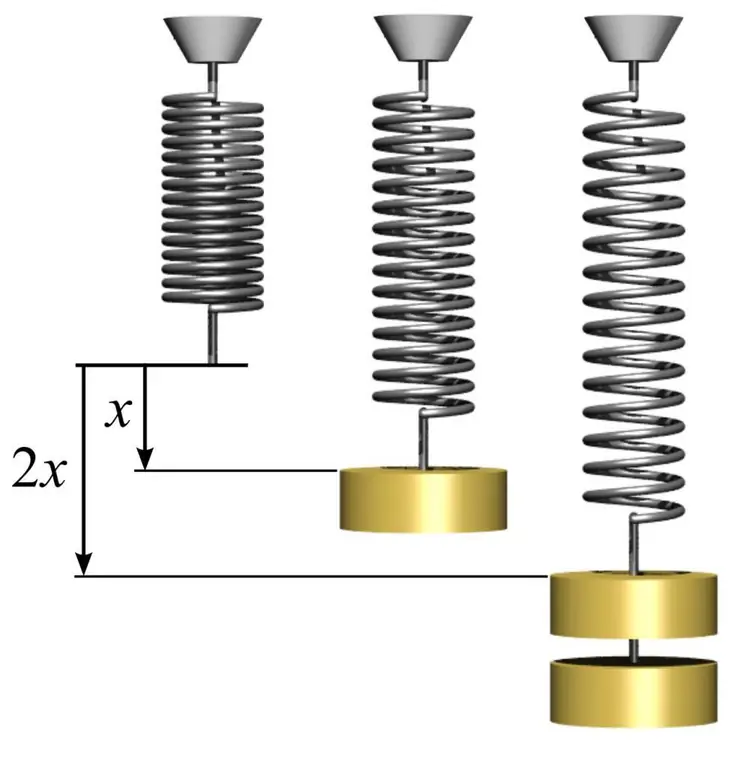
Om die elastisiteitsmodulus te bepaal, asook om te verstaan hoe om dit te gebruik, kan jy 'n eenvoudige voorbeeld met 'n veer gee. Om dit te doen, moet jy 'n metaalveer neem en die oppervlakte van die sirkel wat sy spoele vorm, meet. Dit word gedoen deur die eenvoudige formule S=πr² te gebruik, waar n pi gelyk aan 3.14 is en r die radius van die spoel van die veer is.
Volgende, meet die lengte van die veer l0 sonder vrag. As jy enige vrag met massa m1 aan 'n veer hang, dan sal dit sy lengte vergroot tot 'n sekere waarde l1. Die elastisiteitsmodulus E kan bereken word gebaseer op die kennis van Hooke se wet deur die formule: E=m1gl0/(S(l) 1-l0)), waar g die vryvalversnelling is. In hierdie geval let ons daarop dat die hoeveelheid vervorming van die veer in die elastiese gebied 1% kan oorskry.
Om die Jong se modulus te ken, stel jou in staat om die hoeveelheid vervorming onder die werking van 'n spesifieke spanning te voorspel. In hierdie geval, as ons nog 'n massa m2 aan die veer hang, kry ons die volgende waarde van relatiewe vervorming: d=m2g/ (SE), waar d - relatiewe vervorming in die elastiese gebied.
Isotropie en anisotropie
Modulus van elastisiteit is 'n eienskap van 'n materiaal wat die sterkte van die binding tussen sy atome en molekules beskryf, maar 'n spesifieke materiaal kan verskeie verskillende Young se moduli hê.
Die feit is dat die eienskappe van elke vaste stof afhang van sy interne struktuur. As die eienskappe dieselfde is in alle ruimtelike rigtings, dan praat ons van 'n isotropiese materiaal. Sulke stowwe het 'n homogene struktuur, so die werking van 'n eksterne krag in verskillende rigtings op hulle veroorsaak dieselfde reaksie van die materiaal. Alle amorfe materiale is isotropies, soos rubber of glas.
Anisotropie is 'n verskynsel wat gekenmerk word deur die afhanklikheid van die fisiese eienskappe van 'n vaste stof of vloeistof van rigting. Alle metale en legerings wat daarop gebaseer is, het een of ander kristalrooster, dit wil sê 'n geordende eerder as 'n chaotiese rangskikking van ioniese kerns. Vir sulke materiale wissel die elastisiteitsmodulus na gelang van die aksie-as van die eksterne spanning. Metale met kubieke simmetrie, soos aluminium, koper, silwer, vuurvaste metale en ander, het byvoorbeeld drie verskillende Young's-moduli.
skuifmodulus
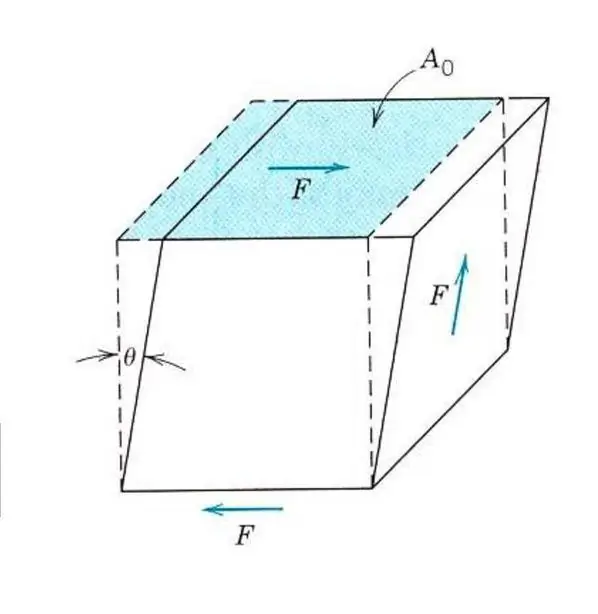
Beskrywing van die elastiese eienskappe van selfs 'n isotropiese materiaal vereis nie kennis van een Young se modulus nie. Omdat, benewens spanning en kompressie, die materiaal deur skuifspannings of torsiespannings beïnvloed kan word. In hierdie geval sal dit anders reageer op eksterne krag. Om elastiese skuifvervorming te beskryf, word 'n analoog van Young se modulus, skuifmodulus of elastisiteitsmodulus van die tweede soort bekendgestel.
Alle materiale weerstaan skuifspannings minder as spanning of kompressie, so die skuifmoduluswaarde vir hulle is 2-3 keer minder as die waarde van Young se modulus. Dus, vir titanium, waarvan die Young se modulus gelyk is aan 107 GPa, is die skuifmodulusslegs 40 GPa, vir staal is hierdie syfers onderskeidelik 210 GPa en 80 GPa.
Modulus van elastisiteit van hout

Hout is 'n anisotropiese materiaal omdat houtvesels in 'n spesifieke rigting georiënteer is. Dit is langs die vesels dat die elastisiteitsmodulus van hout gemeet word, aangesien dit 1-2 grootteordes kleiner oor die vesels is. Kennis van Young se modulus vir hout is belangrik en word in ag geneem wanneer houtpaneelstrukture ontwerp word.
Die waardes van die elastisiteitsmodulus van hout vir sommige soorte bome word in die tabel hieronder getoon.
| Boomaansig | Young se modulus in GPa |
| lourierboom | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Spruce | 11 |
| Pine | 10 |
| Oak | 12 |
Daar moet kennis geneem word dat die waardes wat gegee word met tot 1 GPa vir 'n spesifieke boom kan verskil, aangesien sy Jong se modulus beïnvloed word deur die digtheid van die hout en groeitoestande.

Skeurmoduli vir verskeie boomspesies is in die reeks van 1-2 GPa, byvoorbeeld, vir denne is dit 1,21 GPa, en vir eikehout 1,38 GPa, dit wil sê, hout weerstaan feitlik nie skuifspannings nie. Hierdie feit moet in ag geneem word by die vervaardiging van houtdraende strukture, wat ontwerp is om slegs in spanning of kompressie te werk.
Elastiese eienskappe van metale
In vergelyking met die Young se modulus van hout, is die gemiddelde waardes van hierdie waarde vir metale en legerings 'n orde van grootte groter, soos in die volgende tabel getoon.
| Metal | Young se modulus in GPa |
| Brons | 120 |
| Copper | 110 |
| Staal | 210 |
| Titanium | 107 |
| Nikkel | 204 |
Elastiese eienskappe van metale wat 'n kubieke singonie het, word beskryf deur drie elastiese konstantes. Sulke metale sluit koper, nikkel, aluminium, yster in. As 'n metaal 'n seskantige singonie het, is ses konstantes reeds nodig om sy elastiese eienskappe te beskryf.
Vir metaalstelsels word Young se modulus binne 0.2% vervorming gemeet, aangesien groot waardes reeds in die onelastiese gebied kan voorkom.






